Preprocesador

El preprocesador fue ideado como un breve script de python para adaptar archivos disímiles a un formato legible por el solver y acabó cubriendo todo lo referido al cálculo de factores de vista.

La malla tridimensional del satélite, junto con los materiales asignados a cada polígono que la compone, son información suficiente para el cálculo de la transmisión de calor por conducción. Estos datos ya se encuentran estructurados de forma tal que es preciso y eficiente considerar solo el aporte de calor de la vecindad para cualquier punto en un tiempo determinado.

En cambio, para la transmisión de calor por radiación, la energía recibida en un punto es el resultado de integrar los rayos que fueron emitidos/reflejados por otros cuerpos (Tierra, Sol) u elementos del mismo satélite. Pese a ello, en el dominio del problema, ni la geometría del satélite, ni las características de los materiales se modifican. Más aún, los rayos viajan por el vacío, con lo que su energía solo disminuye con los rebotes. Estas simplificaciones permiten transformar la integración del efecto de rayos individuales en flujos constantes de energía en función de factores de vista entre elementos y los astros. De forma tal que conducción y radiación puedan resolverse homogéneamente con operaciones matriciales en el solver. Como ventaja adicional, la magnitud del aporte energético se separa de la proporción que se esperaría que un cuerpo reciba de otro, permitiendo reutilizar parámetros geométricos en distintos escenarios físicos.

El factor de vista es un concepto central en muchos de los modelos de cálculo de radiación y puede entenderse coloquialmente como la proporción del campo de vista que cubre una superficie respecto a otra.

El método Monte Carlo permite definir y aproximar factores de vista con mayor precisión. En él se seleccionan puntos del elemento emisor y direcciones al azar en la que se emiten rayos, se toma registro de los elementos impactados y luego se computa el factor de vista como la razón entre los rayos impactados y el total de rayos emitidos. Dependiendo del propósito de la simulación, se pueden emitir rayos desde un elemento en todas las direcciones, como si fuese una placa, o solo en dirección de la normal, suponiendo que es parte de un cuerpo sólido. También pueden introducirse reflexiones reemitiendo rayos desde las posiciones de impacto.

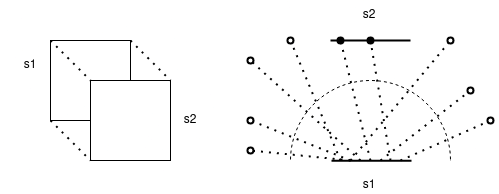
En el ejemplo de la figura se disparan diez rayos desde \(s1\), de los cuales solo dos impactan \(s2\), por lo que el factor de vista entre \(s1\) y \(s2\) se aproximaría como \(\frac{2}{10}\). Notar que si \(s1\) y \(s2\) no tuviesen la misma área, el factor de vista \(s1s2\) diferiría del factor de vista \(s2s1\). Si se tratasen de dos cuerpos negros, la energía que \(s1\) aporta a \(s2\) podría calcularse como el producto entre el total de energía emitida por \(s1\) y el factor de vista \(s1s2\).

Para introducir el efecto de los materiales sobre la reflexión se evaluaron dos enfoques:

• Enfoque A: Considerar la pérdida de energía por rayo en cada rebote de acuerdo con las características del material y desaparecer al no sobrepasar un nivel de energía despreciable cutoff.

• Enfoque B: Utilizar números pseudoaleatorios para decidir si un elemento absorbe o no a un rayo y solo contar al elemento que finalmente lo absorbió.

Se optó por el enfoque B, dado que si bien el enfoque A producía resultados más precisos para pocos rayos, acababa por disparar mayor cantidad de rayos al ser más frecuentes las reflexiones. Además, fue más sencillo pensar el efecto de los materiales sobre rayos individuales.

En las siguientes secciones se especifica la implementación de cada interacción en la que se descompone el cálculo de transmisión de calor por radiación.