Agni B3V es una solución integral para el modelado, simulación e interpretación de los fenómenos térmicos que afectan a los satélites.

Actualmente incluye herramientas para:

Construcción modelos tridimensionales de satélites a través de la unión de primitivas o uniendo vértices manualmente. Remallado automático para mejorar resultados de FEM. (FreeCAD)
Asignación de materiales y condiciones a distintas partes del modelo. (FreeCAD Agni B3V Addon)
Configuración de constantes orbitales, como ser radiación infraroja terrestre, albedo y constante solar. (GMAT)
Estimación de factores de vista e intercambio de energía entre elementos y entre elementos y otros cuerpos celestes. (Preprocesador)
Simulación térmica segundo a segundo en un intervalo y órbita especificados. (Solver)
Postprocesado e interpretación de resultados. (Paraview, Plotter)

Workflow general

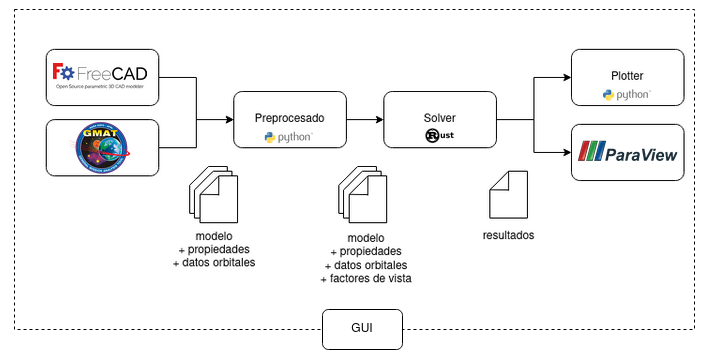
Cada una de estas herramientas pueden ser utilizadas de manera independiente o en conjunta a través de la Interfaz de Usuario.

Índice

La documentación se divide en las siguientes secciones:

Consideraciones

En el estado actual del sistema solo se permiten orbitas circulares y aptitud del satélite Sun Pointing.

Se deja a discreción del usuario la verificación de la precisión de los resultados generados por el presente software por fuera de los benchmarks, especialmente en el cálculo del albedo. Se recomienda utilizar el software con cautela.

Desarrollo y Uso

El código del proyecto puede ser encontrado en su repositorio de GitHub.

Para instrucciones detalladas sobre cómo instalar y ejecutar el software como desarrollador, consulte las pautas adjuntas en el repositorio.

Para instalar AgniB3V como usuario final, se recomienda leer las instrucciones de instalación en la sección correspondiente del manual del usuario.

Autores

Este trabajo fue realizado bajo el marco del Trabajo Profesional de Ingeniería Informática de la Univesidad de Buenos Aires.

Los integrantes del equipo son:

Barreneche Franco
Belinche Gianluca
Botta Guido
Ventura Julian

Manual de Usuario

En el manual de usuario se tratarán los siguientes temas:

Instalación

Se provee un instalador para el software, el cual puede ser encontrado en el último release del repositorio del proyecto. Este software fue probado para el sistema operativo Ubuntu 22.04 LTS.

Para realizar la instalación, descargar el archivo AgniB3V-v1.0.0.zip y moverlo al directorio deseado. Hacer click derecho sobre alguna región vacía del directorio actual y elegir la opción "Abrir en una terminal". En la terminal, escribir uno a uno los siguientes comandos:

unzip AgniB3V-v1.0.0.zip -d Agni
cd Agni
bash install

Tras haber finalizado la instalación, se podrá iniciar AgniB3V haciendo click derecho sobre el archivo AgniB3V y seleccionando "Ejecutar como Programa".

Errores conocidos

Si se experimentan errores al momento de ejecutar el solver, puede seguir las siguientes instrucciones:

En primer lugar, asegurese de contar con los últimos drivers instalados para su proveedor de tarjeta gráfica. Obtenga los drivers para AMD o Nvidia de fuentes oficiales.

Si los problemas persisten, puede que requiera proveer permisos de administrador a AgniB3V. Para esto deberá ejecutar el archivo AgniB3V-root e ingresar la contraseña del usuario administrador cuando le sea solicitado.

Interfaz de Usuario

Ejecución manual

Para la ejecución manual de la interfaz de usuario, se debe ejecutar el siguiente comando en la ubicación del ejecutable:

python3 main.py

Creación de un nuevo proyecto

La interfaz de usuario permite la creación de proyectos y la utilización de las distintas herramientas del paquete. Al iniciar la aplicación, se abrirá la siguiente pantalla:

En esta se podrá seleccionar el directorio de un proyecto existente o crear uno nuevo. En caso de crear uno nuevo, se deberá seleccionar un directorio y completar el nombre del proyecto.

Al crear un nuevo proyecto, se creará un directorio con el nombre elegido en la carpeta seleccionada. Dentro de este nuevo directorio, se encontrarán dos templates que facilitarán la utilización de gmat y de freecad, como se puede ver en la siguiente pantalla.

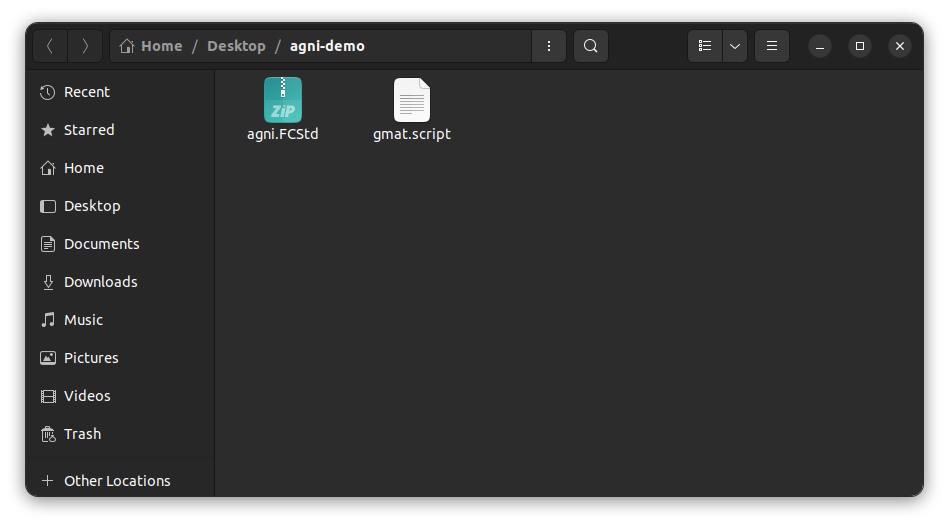
agni.FCStd: es un template de documento que facilita la utilización de freecad. Trae inicializada la configuración para agilizar la utilización del workbench.
gmat.script: es un template de script que facilita la utilización de gmat. Trae por default una órbita ya definida, que puede ser modificada desde GMAT. También trae configurado la generación de los archivos de salida ReportFile.txt y EclipseLocator.txt, que son necesarios para la ejecución del preprocesador.

Ventana de proyecto

Al abrir o crear un proyecto, nos encontraremos con la siguiente ventana:

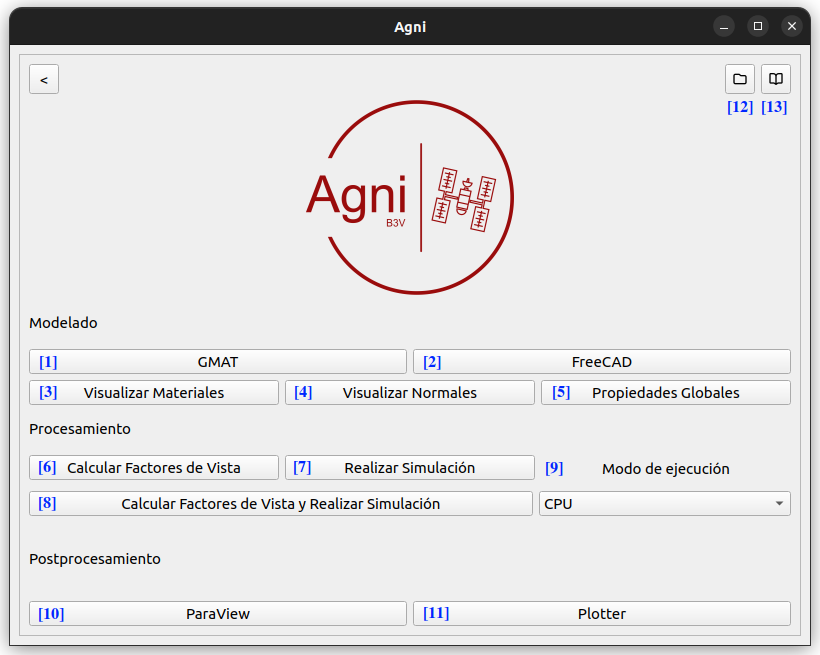
[1]: Abre GMAT con el script gmat.script cargado.
[2]: Abre FreeCAD con el documento agni.FCStd cargado.
[3]: Abre el visualizador de materiales. Requiere de los archivos mesh.vtk y properties.json, generados en FreeCAD.
[4]: Abre el visualizador de normales. Requiere de los archivos mesh.vtk y properties.json, generados en FreeCAD.
[5]: Abre la ventana de configuración de propiedades globales. Requiere del archivo properties.json, generado en FreeCAD.
[6]: Ejecuta el preprocesador. Requiere de los archivos mesh.vtk y properties.json, generados en FreeCAD; y de los archivos ReportFile.txt y EclipseLocator.txt, generados en GMAT.
[7]: Ejecuta el solver. Requiere de los archivos mesh.vtk, generado en FreeCAD; view_factors.vf, generado por el procesador; y properties.json, modificado por el preprocesador.
[8]: Ejecuta el preprocesador y, al finalizar, ejecuta el solver. La ejecución de este comando bloquea por completo la utilización de la interfaz gráfica hasta la finalización de los procesos.
[9]: Permite la selección del modo de ejecución entre CPU y GPU para la ejecución del solver.
[10]: Abre ParaView con los resultados cargados. Requiere del directorio /results, generado por el solver.
[11]: Abre el plotter con los resultados cargados. Requiere del directorio /results, generado por el solver.
[12]: Abre el directorio del proyecto.
[13]: Abre la documentación en una nueva pestaña del navegador predeterminado.

GMAT

GMAT (General Mission Analysis Tool) es un sistema de software de código abierto, empresarial y multi-misión para el diseño, optimización y navegación de misiones espaciales. El sistema admite misiones en regímenes de vuelo que van desde la órbita terrestre baja hasta misiones lunares, puntos de libración y misiones en el espacio profundo. GMAT es desarrollado por un equipo de la NASA, la industria privada, contribuyentes públicos y privados, y se utiliza para el soporte de misiones del mundo real, estudios de ingeniería, como herramienta educativa y participación pública. GMAT contiene modelos de objetos del mundo real, como naves espaciales y propulsores, y "objetos" de análisis, como propagadores, gráficos e informes. Estos objetos se utilizan en una secuencia de misión en la que el usuario emplea comandos respaldados por el sistema para modelar eventos de la misión y realizar estimaciones.

Para más información, visitar https://documentation.help/GMAT/WelcomeToGmat.html

Instalación manual

La instalación de GMAT viene incluida en la instalación del paquete de AgniB3V. Sin embargo, si desea instalar manualmente GMAT, puede hacerlo desde la página web https://sourceforge.net/projects/gmat/.

Tutoriales

Se recomienda seguir los tutoriales de GMAT para familiarizarse con la aplicación. Para ello visitar https://documentation.help/GMAT/Tutorials.html.

GMAT en Agni

Agni B3V, como se menciona en la sección Interfaz de Usuario, provee un template de script de GMAT que contiene una misión por defecto, la cual puede ser adaptaba según las necesidades del usuario.

Al abrir GMAT desde la interfaz de usuario, se cargará la misión por defecto que trae el script y se verá la siguiente ventana:

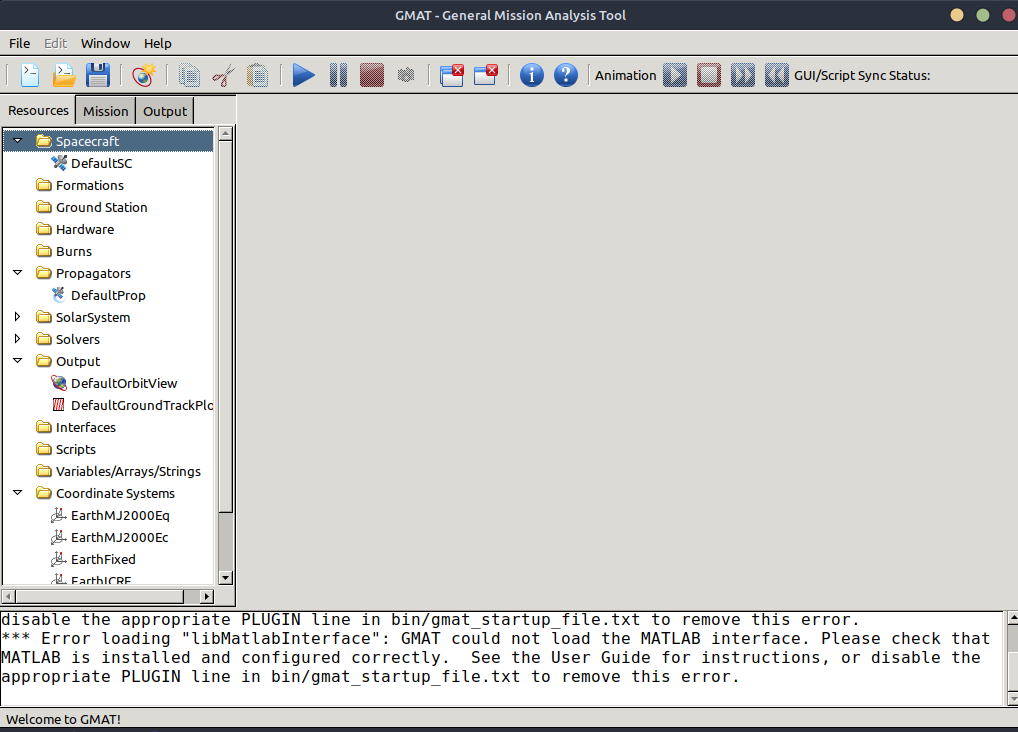
En las secciones de "Resources", "Mission" y "Output" se podrán modificar las condiciones que sean necesarias. Se recomienda no modificar la ruta de salida de los archivos ni los archivos generados, ya que puede alterar el correcto funcionamiento de las siguientes etapas.

Una vez configurada la misión, se debe hacer click en el botón para correr la misión:

Al completarse la simulación, se podrá ver la órbita para poder validar visualmenta la correctitud de la órbita configurada.

Además, se generarán dos archivos de salida en la ruta del proyecto:

ReportFile.txt: Incluye los datos de la órbita a lo largo del tiempo, como la posición del satélite y del sol con respecto a la tierra.
EclipseLocator.txt: Contiene la información del momento en el que transcurre un eclipse y su duración.

FreeCAD

FreeCAD es una aplicación libre de diseño asistido por computadora. Es la aplicación recomendada para el desarrollo de modelos ya que permite una fácil integración con el paquete proporcionado. Para más información, visitar https://www.freecad.org/.

FreeCAD se encuentra bajo una licencia LGPL2+. La licencia se encuentra en https://github.com/FreeCAD/FreeCAD/blob/main/LICENSE. Para más información, visitar https://wiki.freecad.org/Licence/en.

Instalación manual

La instalación de FreeCAD viene incluida en la instalación del paquete de AgniB3V. Sin embargo, si desea instalar manualmente FreeCAD, puede hacerlo desde la página web https://www.freecad.org/downloads.php.

Modelado

A continuación se mostrará un ejemplo sencillo de modelado con el objetivo de contar con un modelo para ejemplificar el uso del addon más adelante.

Al abrir FreeCAD se encontrará con la siguiente ventana:

Para comenzar, se debe ir al workbench Part.

Aquí se encontrarán elementos para crear como cubos, cilindros, esferas, etc. Se crearán tres elementos, un cubo, un toro y un cilindro.

Para mover los elementos, se debe seleccionar uno de ellos, hacer click derecho y presionar en "Transform".

Una vez movidos, se verá un resultado como el siguiente:

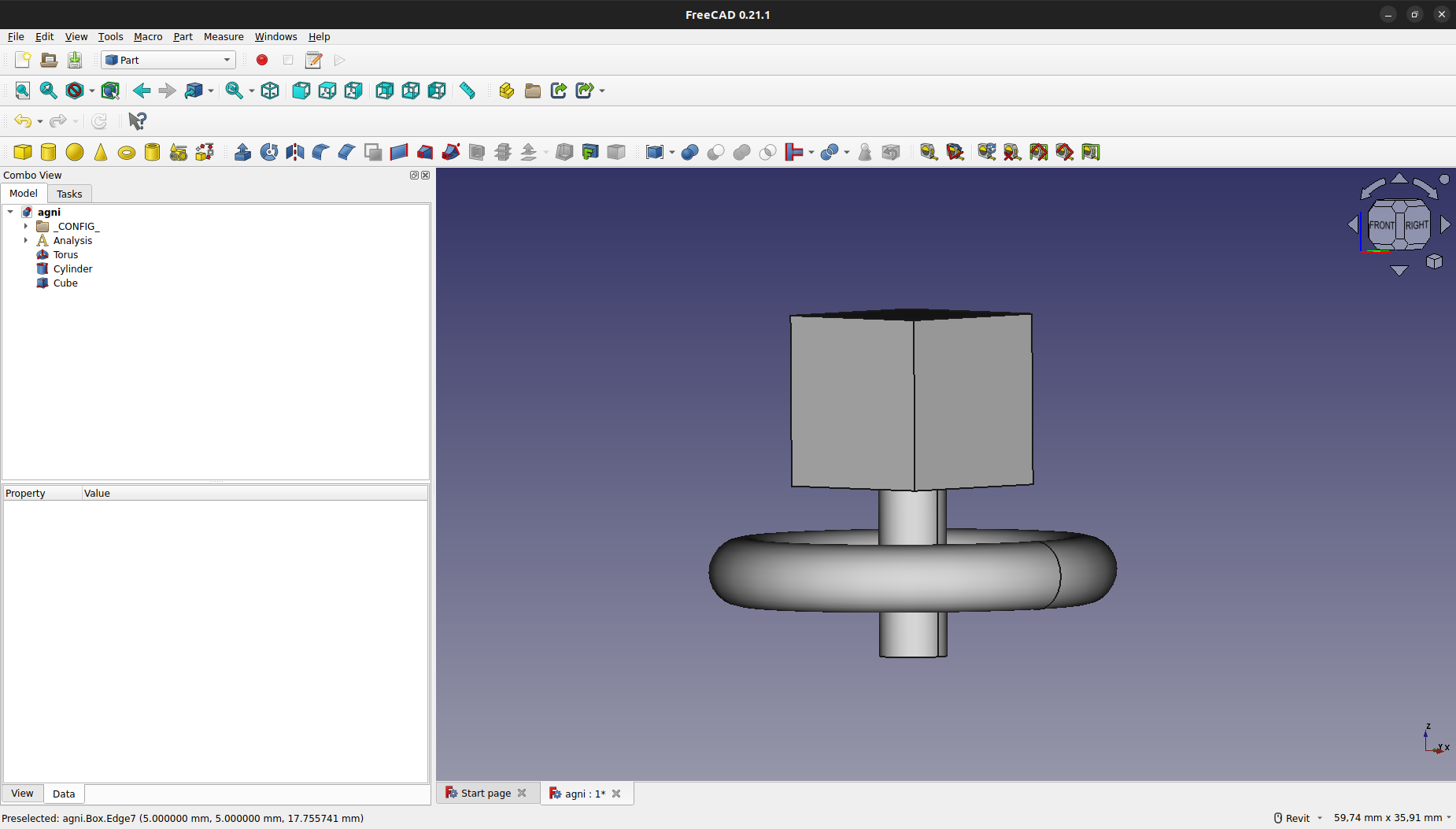
Para cambiar el tamaño de los elementos, se debe seleccionar en el elemento deseado y, en la pestaña de "Data", variar radio, longitud, entre otros.

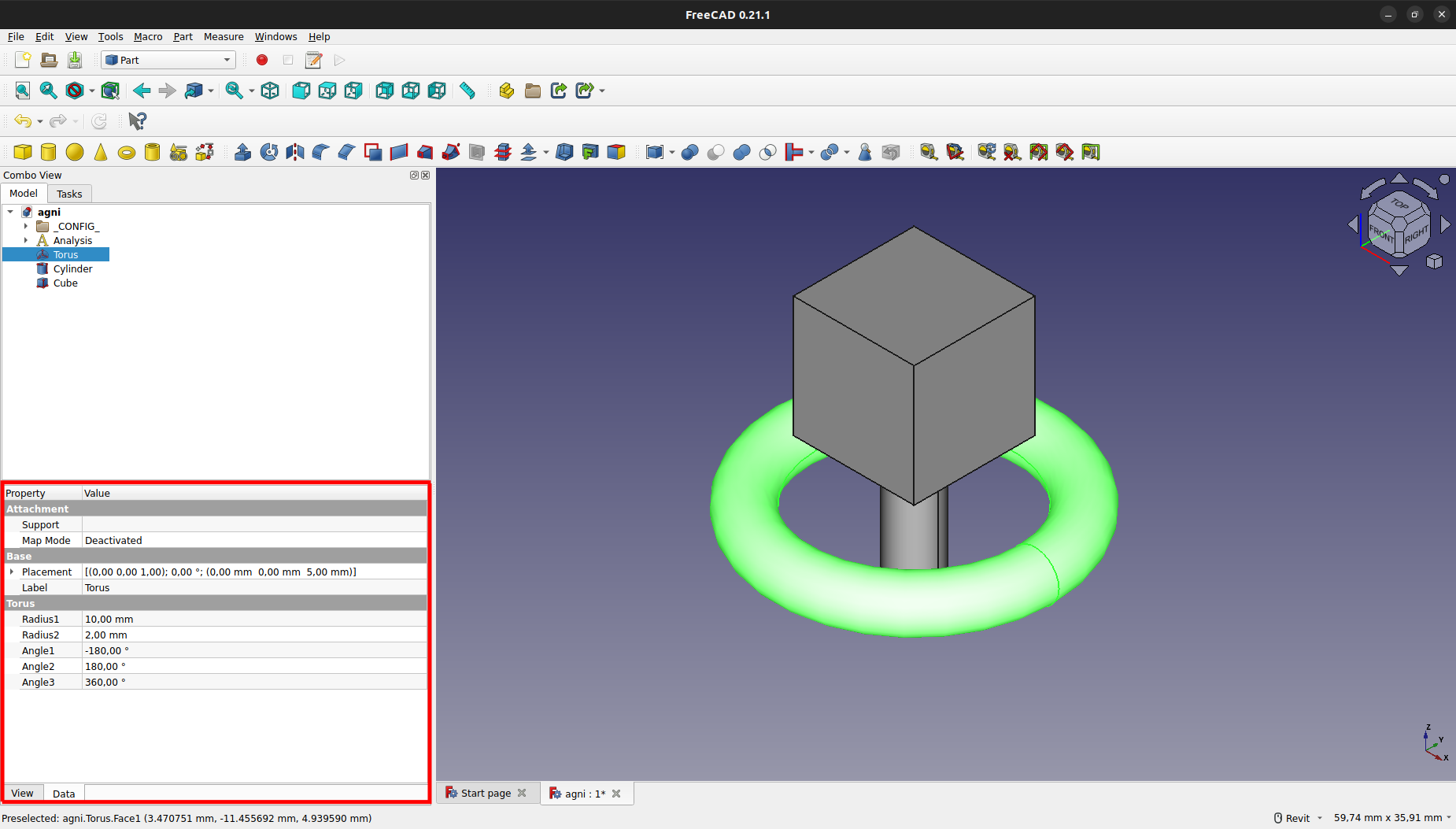
En este caso, se varió el radio del toro, obteniendo el siguiente resultado:

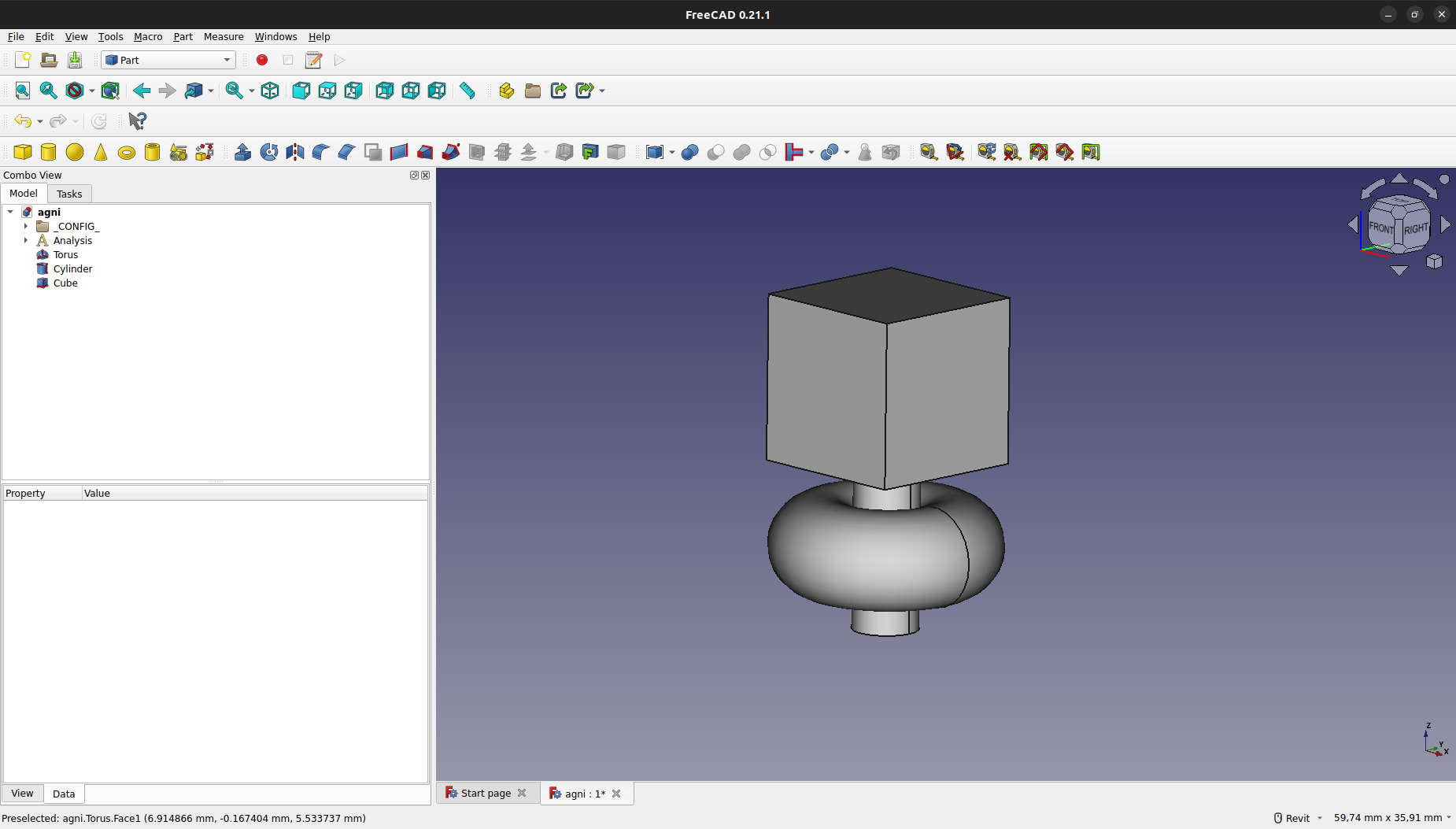
Una vez posicionados y redimensionados los elementos, se seleccionarán:

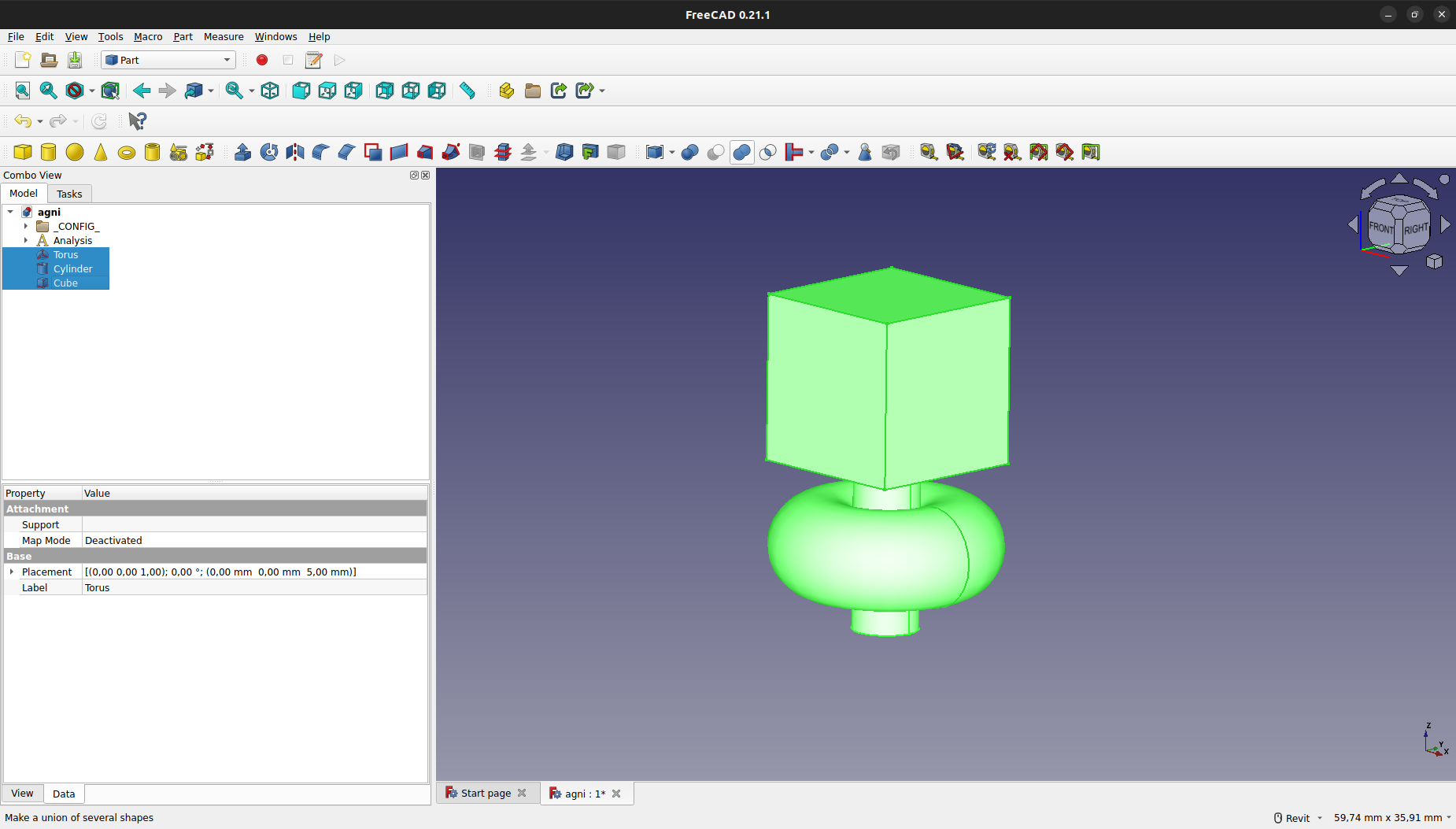
Y, a continuación, se crearán un "Fusion" y un "Boolean Fragments".

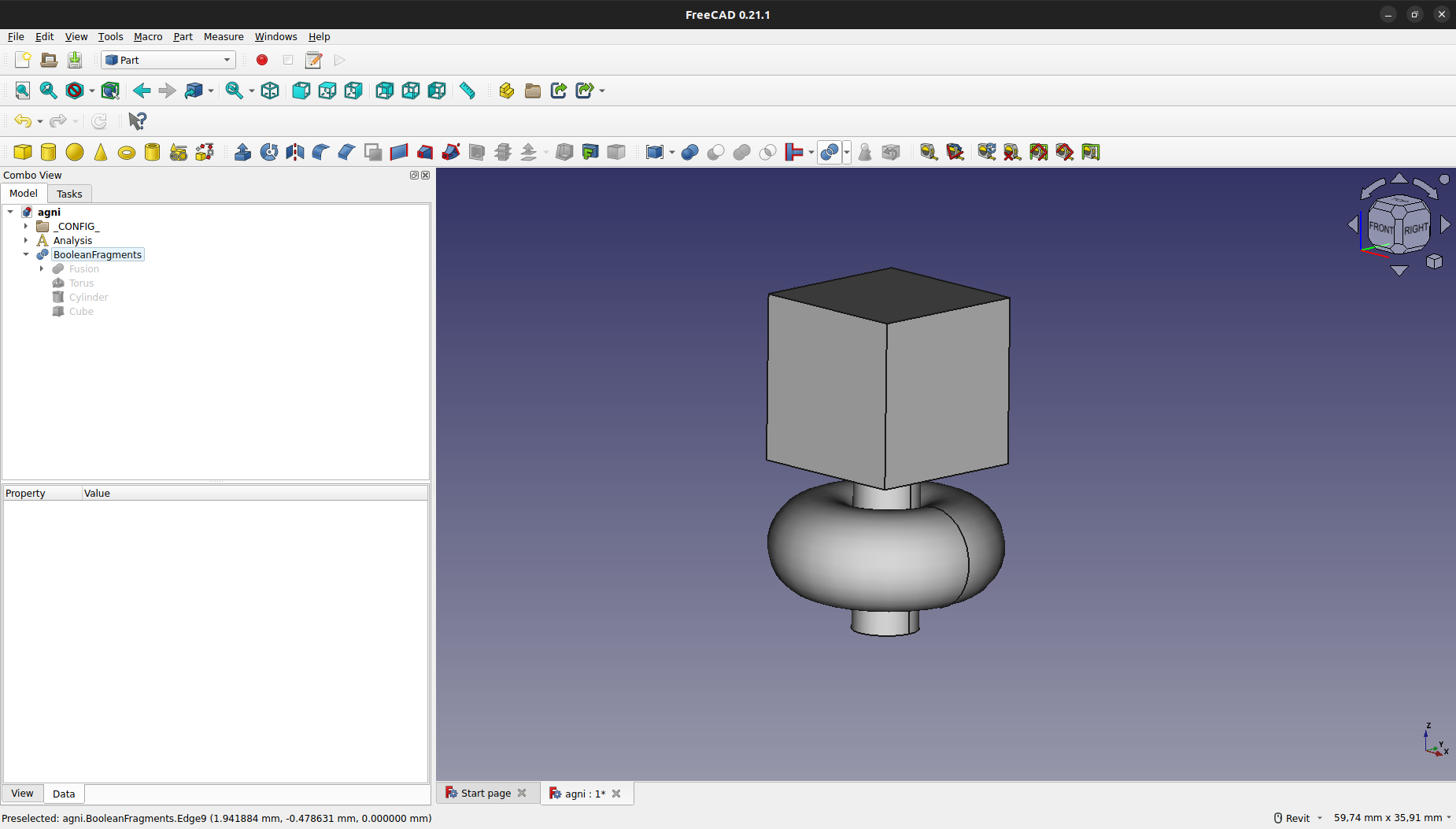
Finalmente, se podrá visualizar el resultado final del modelo básico creado:

Macro WorkFeature (recomendada)

Se recomienda el uso de la macro WorkFeature para la verificación de la orientación de las normales en tiempo de modelado. Para su instalación y tutoriales visitar https://github.com/Rentlau/WorkFeature/tree/master.

Tutoriales

Para profundizar en la realización de modelos más complejos, se recomienda buscar entre los diversos tutoriales que hay en la wiki de freecad, los foros de freecad y youtube. Se brindan algunos enlaces para comenzar:

Agni Addon

Para facilitar el uso de las herramientas que permiten realizar y visualizar una simulación térmica satelital, se ofrece un addon para FreeCAD. Este agrega un nuevo workbench, cuyo uso se detallará a continuación.

Prerrequisito

Para la utilización completa del workbench, es necesario haber creado un modelo con anterioridad. Si aún no completó este paso, vaya a la sección de Modelado.

Creación de Mallado FEM

Para la creación de un mallado FEM, se debe seleccionar el objeto del modelo y presionar en el botón del mallado, como se ve a continuación:

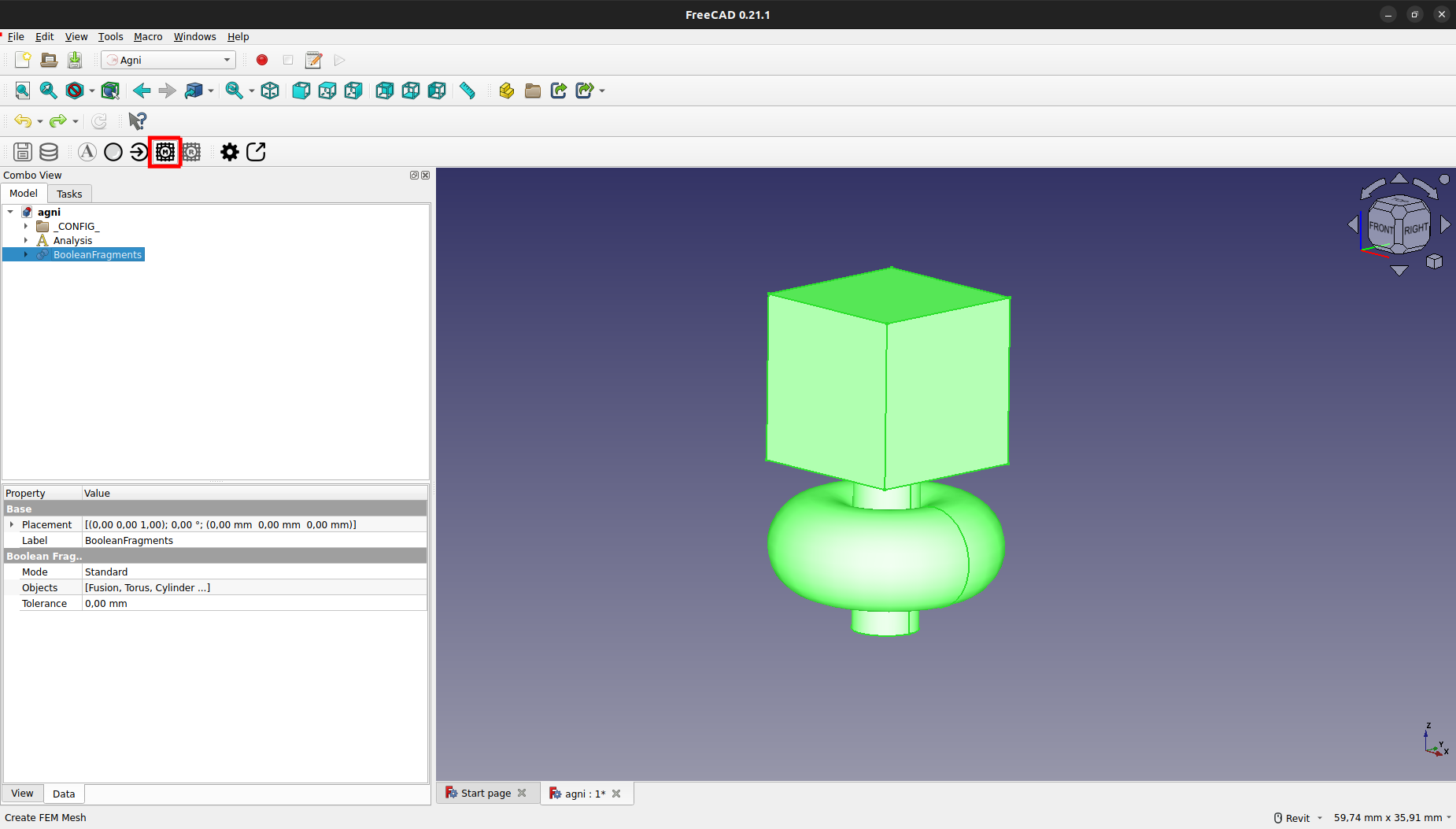
Esto generará automáticamente una malla de triángulos bidimensionales de primer orden, tal cual requiere el sistema para funcionar correctamente. La malla se creará bajo el grupo "Analysis" con el nombre "<nombre_objeto>_Mesh", en este caso "BooleanFragments_Mesh".

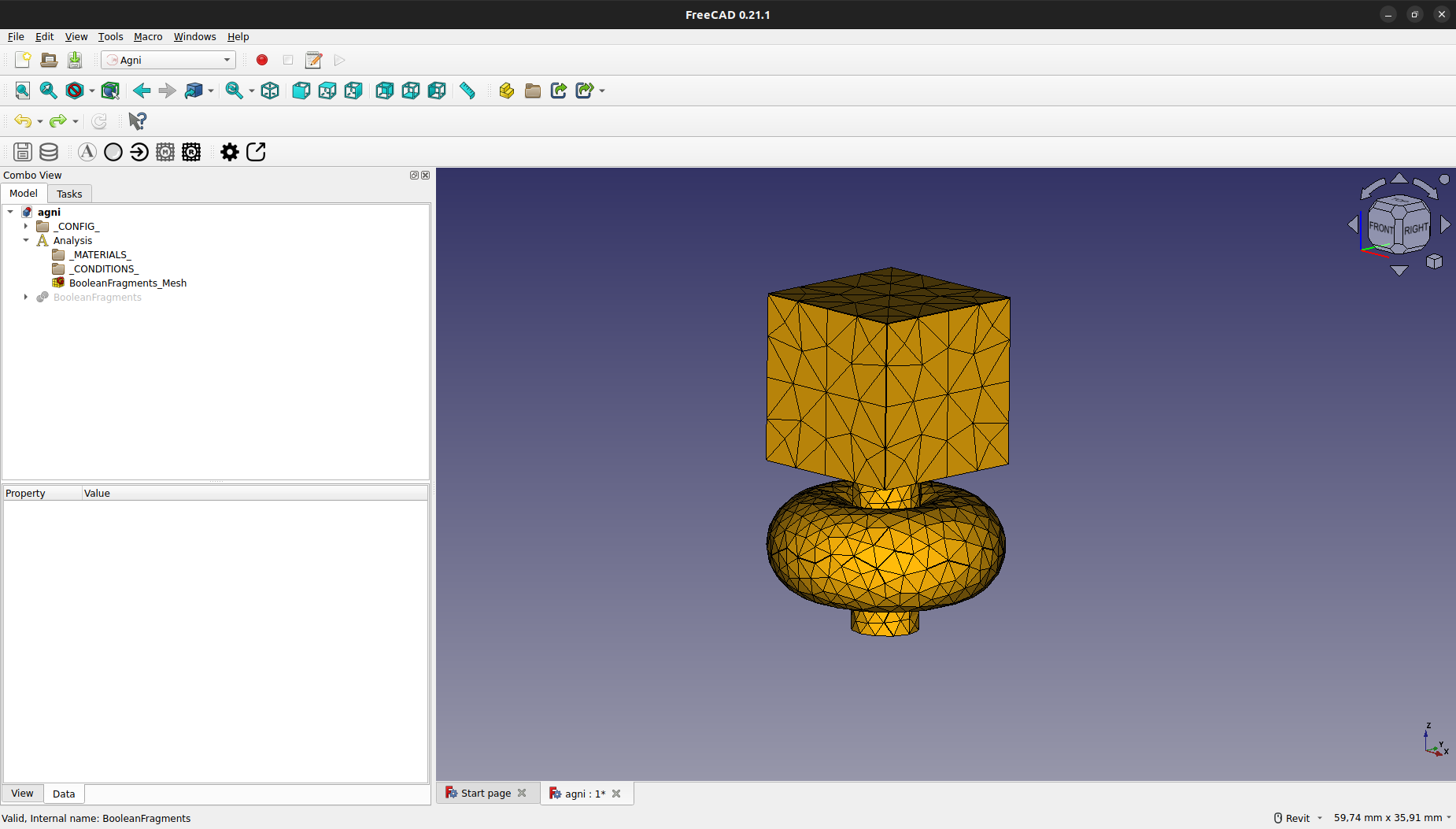
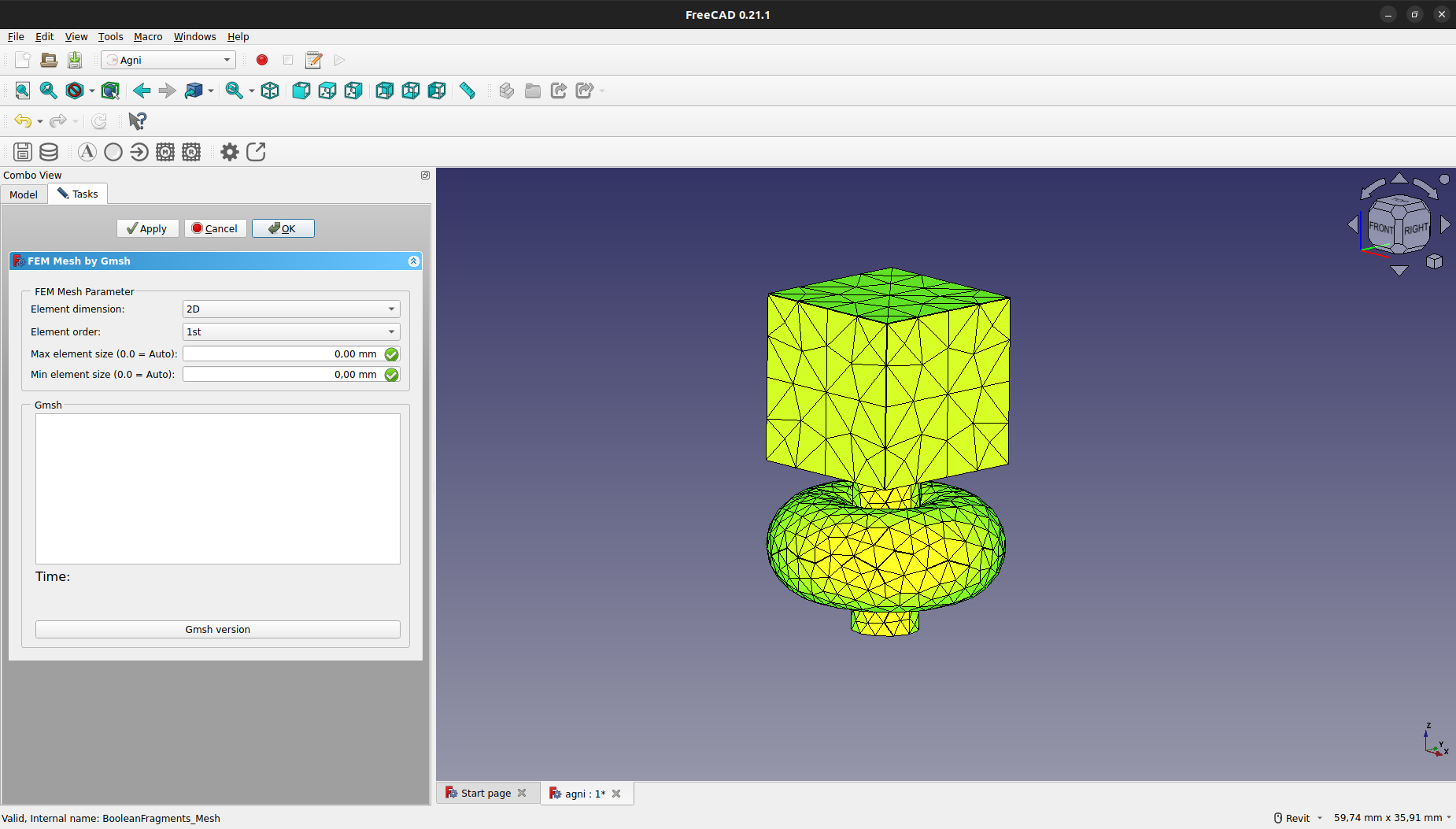
Si se hace doble click en el objeto de la malla, se abrirá un cuadro el cual permite editar el tamaño máximo y mínimo de elemento. En caso de cambiar uno de estos parámetros, se debe recrear la malla presionando el botón "Apply".

Es importante no cambiar los valores de "Element dimension" y "Element order" para garantizar el correcto funcionamiento del sistema.

Regiones

Es posible crear regiones para darle un mayor o menor detalle a las distintas superficies o sólidos del modelo. Para ello, se debe presionar el botón de creación de regiones, como se indica a continuación:

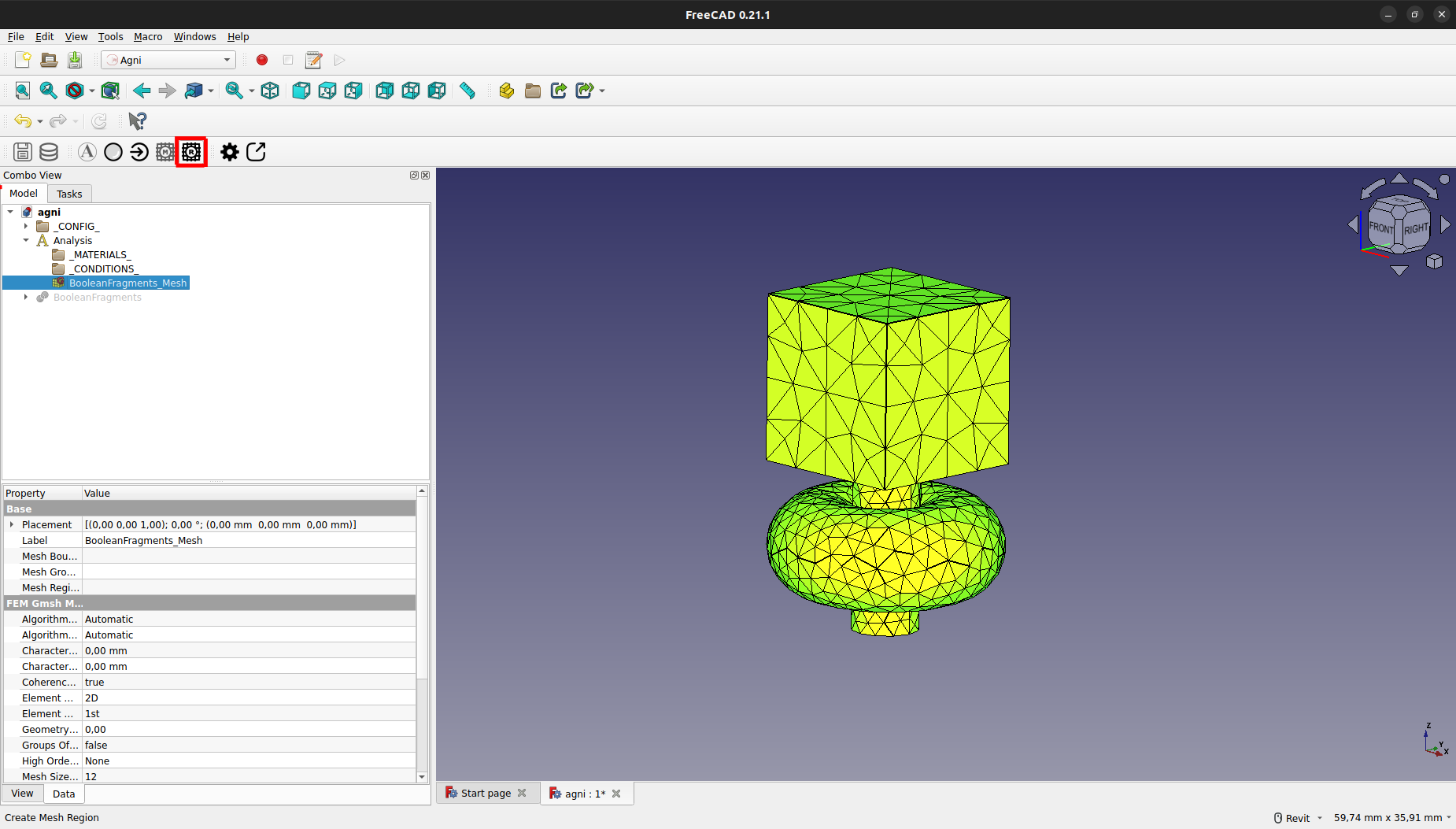
La región se creará bajo el grupo de la malla, con el nombre de "MeshRegion" o "MeshRegionNNN" si hay más de una región.

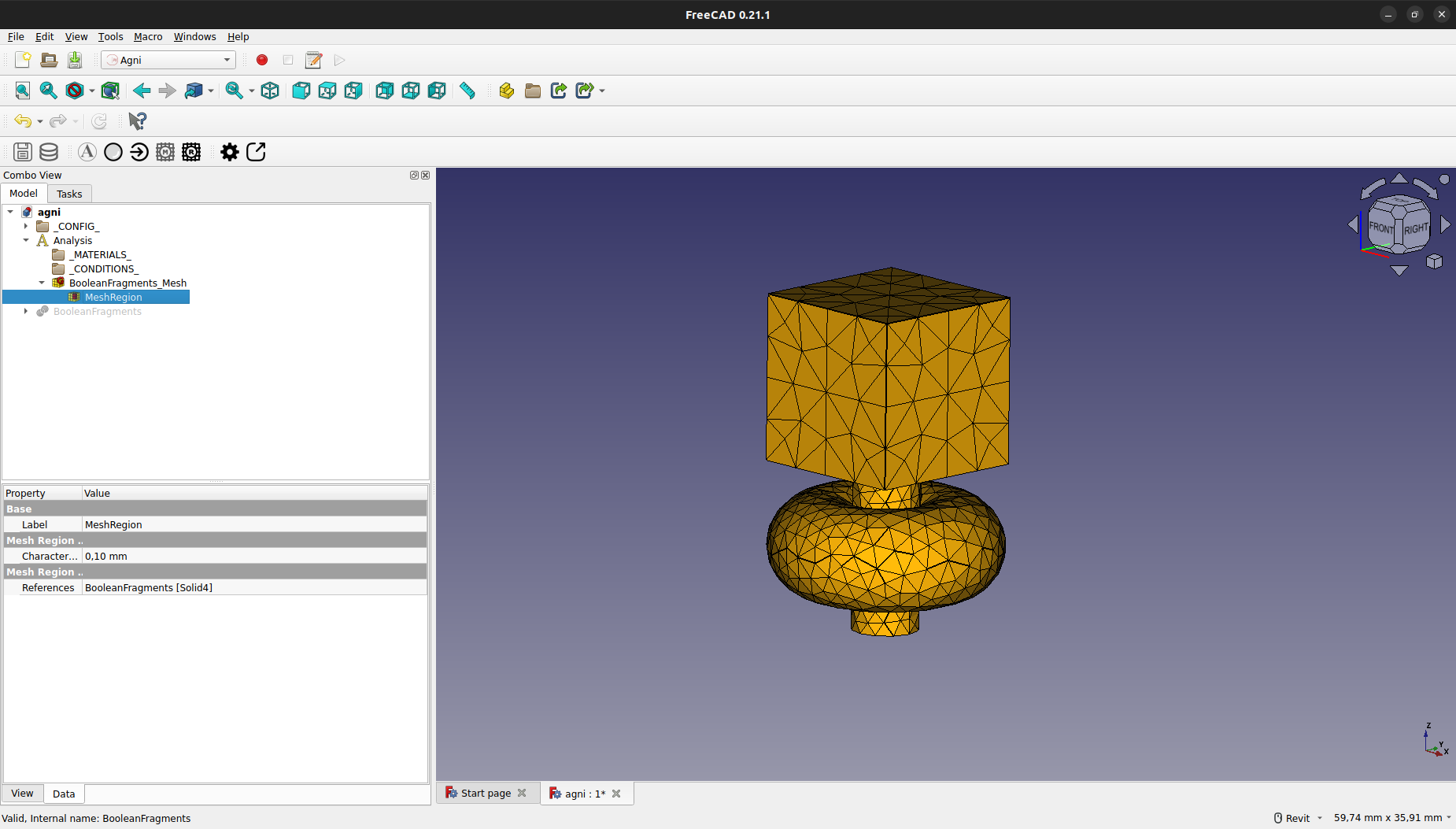
Al hacer doble click sobre la región creada se abrirá un cuadro el cual permite editar el máximo tamaño de elemento y sobre qué región queremos aplicar esta restricción.

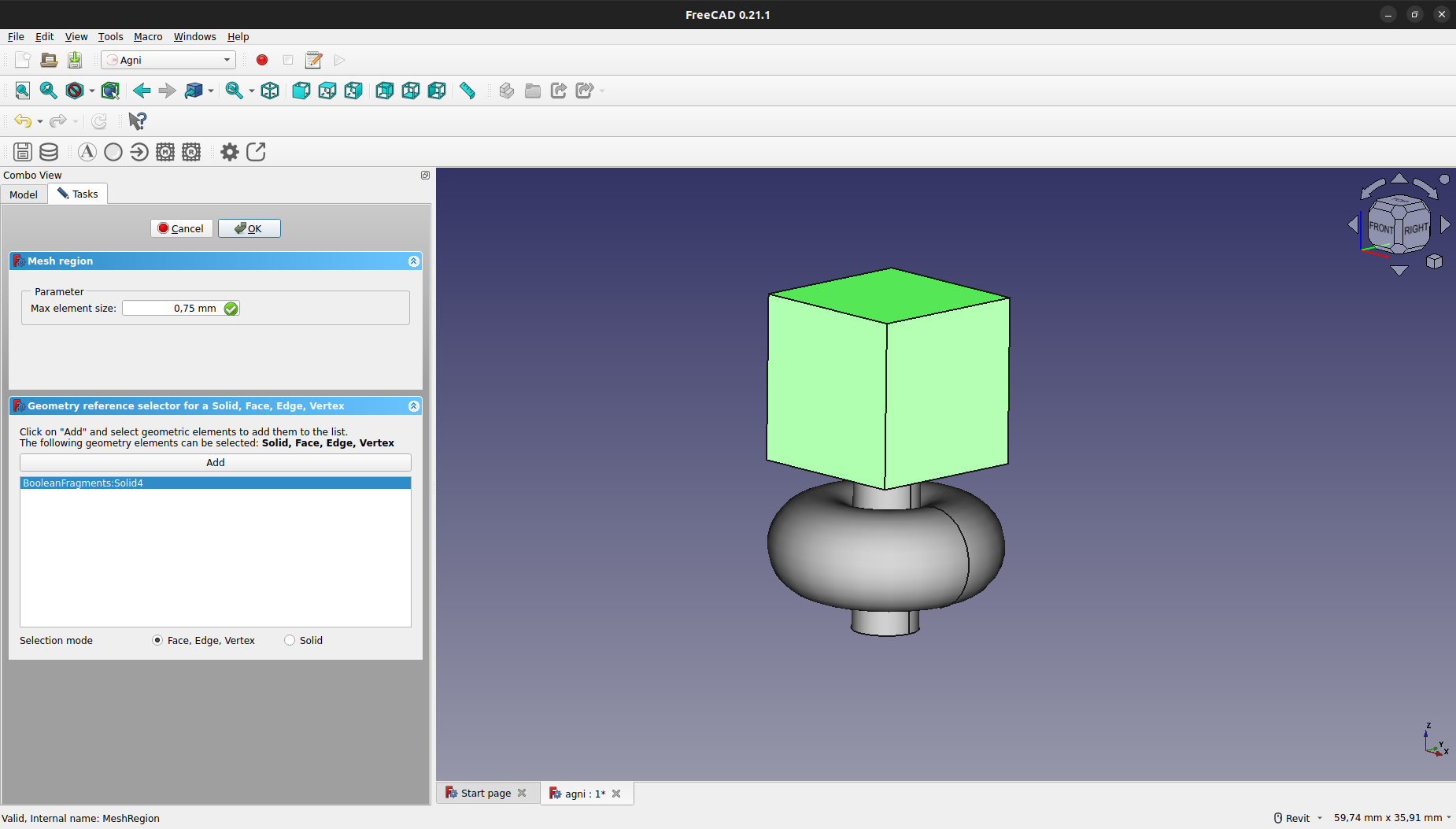
Una vez aplicada la restricción, se debe apretar "OK", volver a abrir el cuadro de y apretar el botón de "Apply" para regenerar la malla con la nueva restricción.

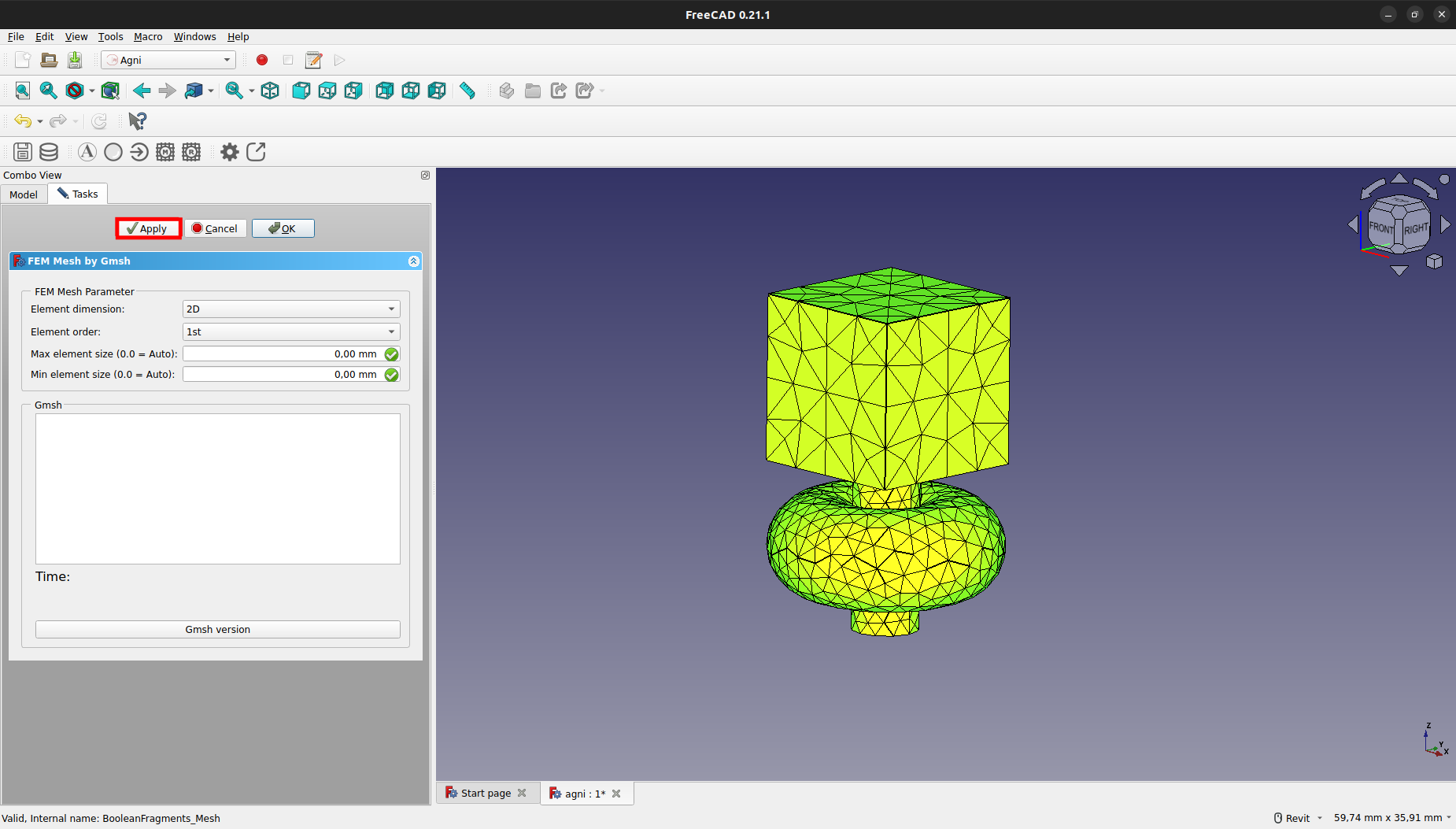
Como se puede ver a continuación, se regeneró la malla con un detalle mucho mayor sobre la región restringida.

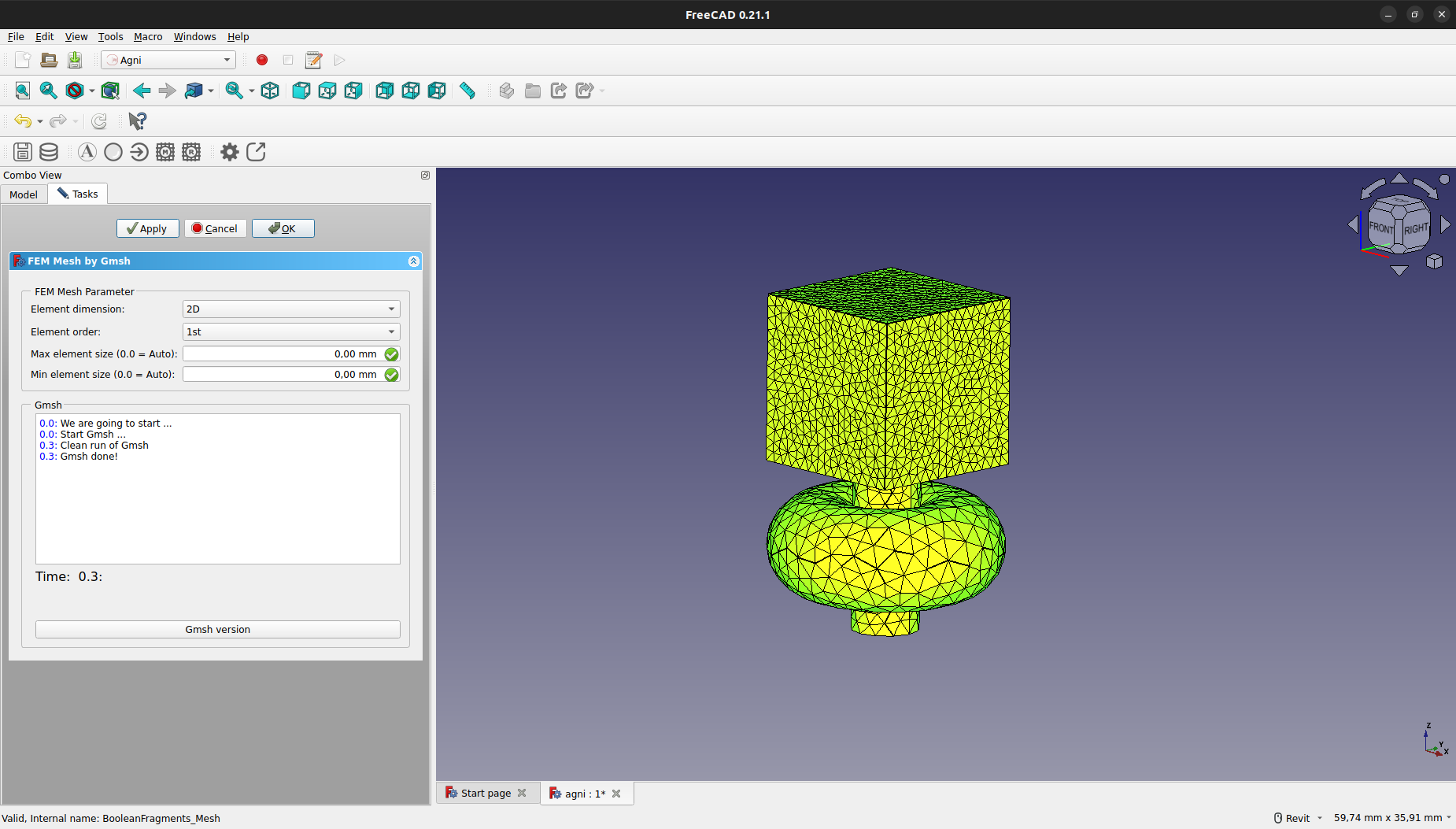
Asignación de Materiales

Para crear un nuevo material, se debe presionar el botón de edición de materiales, como se muestra a continuación:

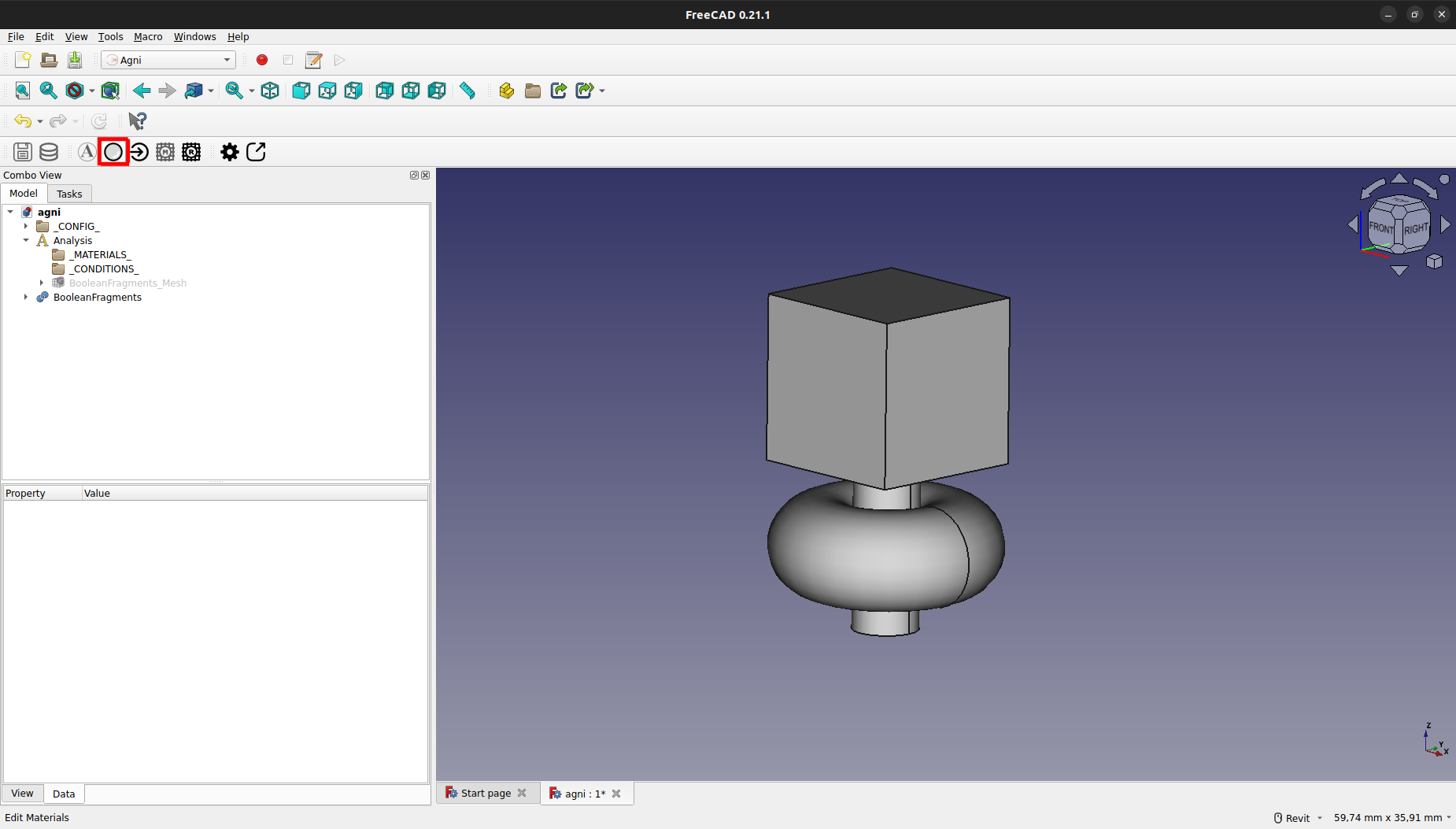
Esto abrirá una ventana con el editor de materiales, en el cual se debe presionar "Add Material" para agregar un nuevo material.

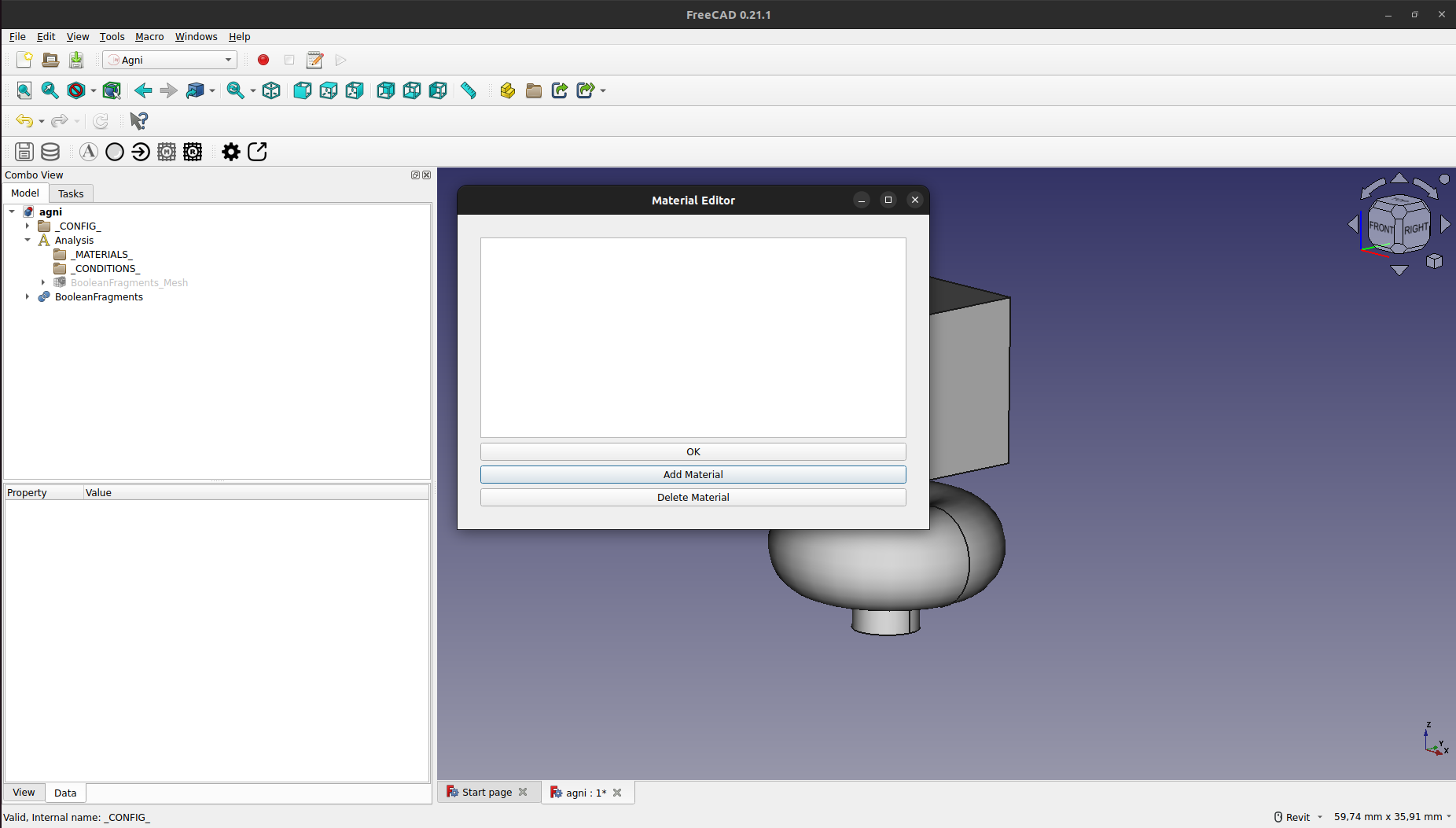
Se debe poner un nombre, "Aluminio" en este caso, y presionar "OK".

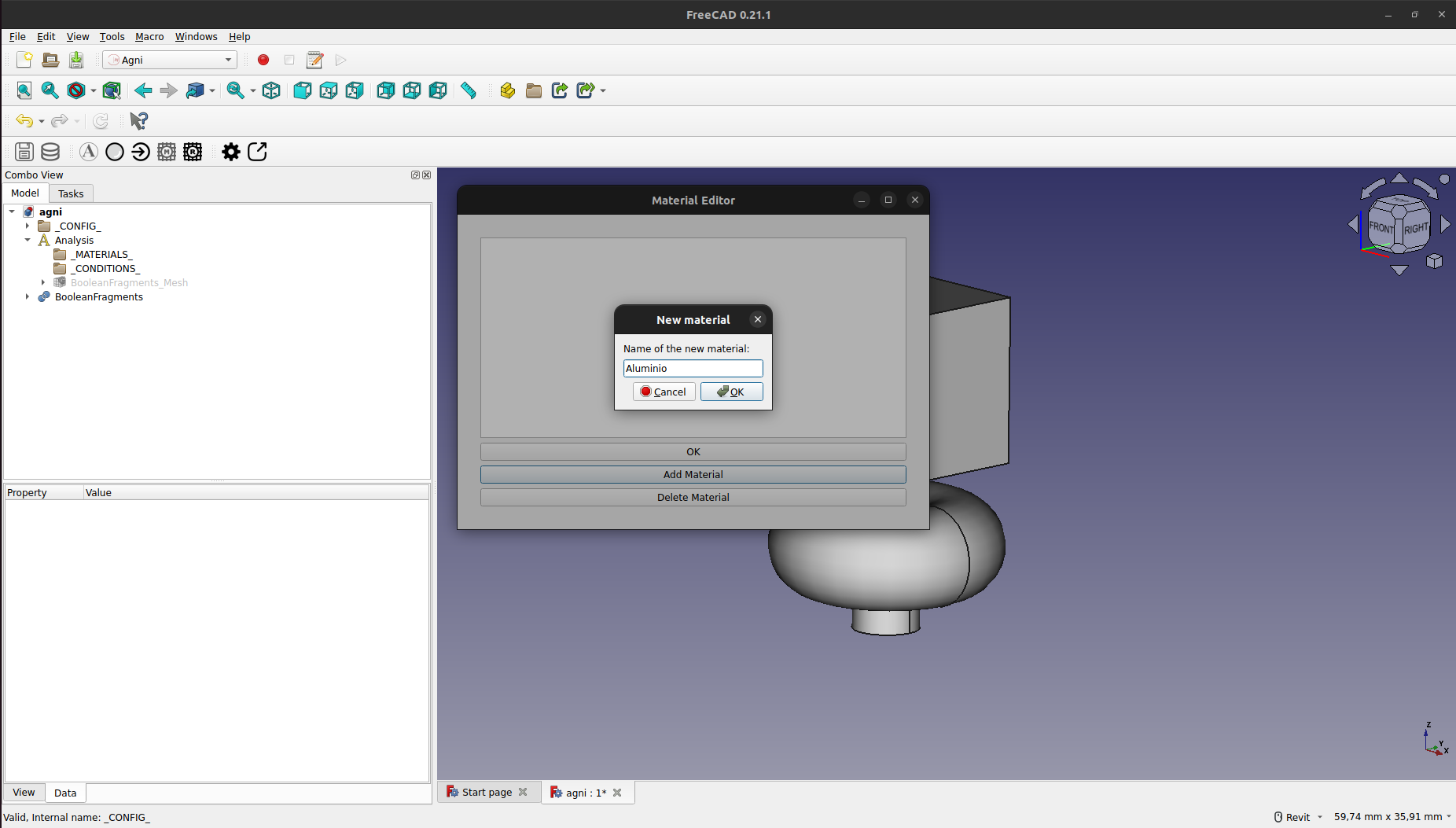
Esto creara el nuevo material, el cual se puede editar presionando sobre el mismo.

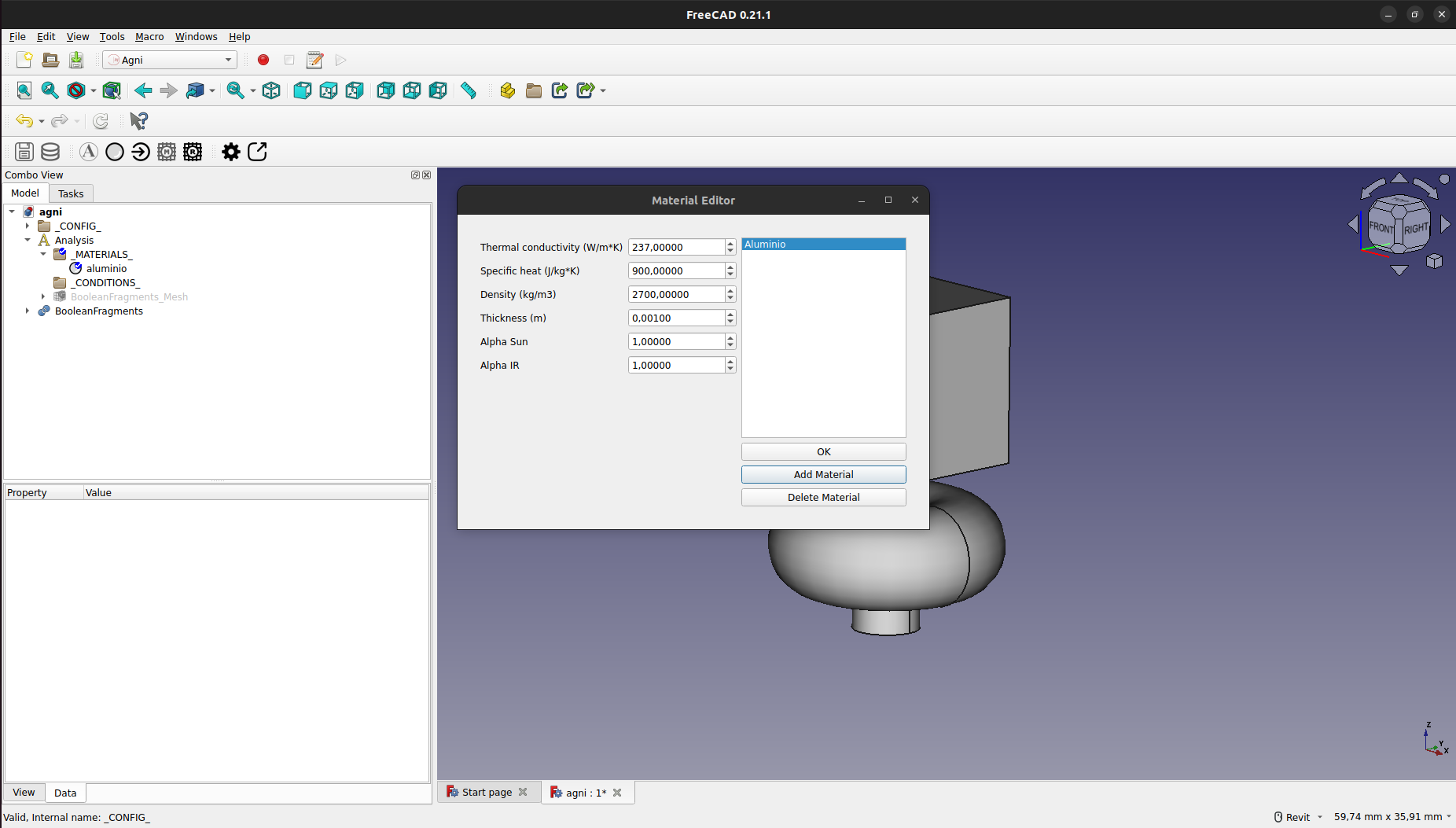
Una vez creado, aparecerá en el panel del modelado con el nombre elegido, bajo el grupo de "_MATERIALS_"

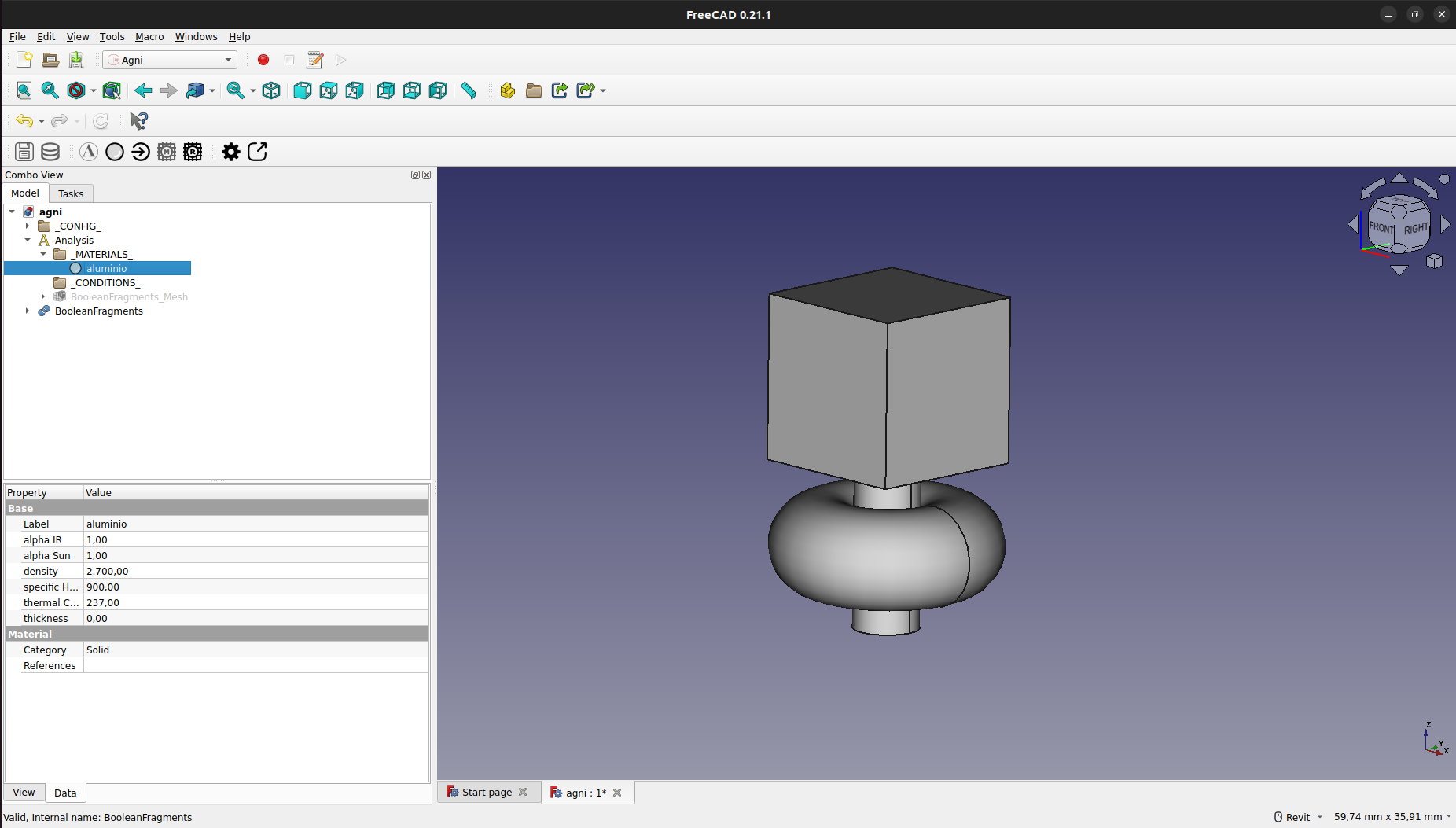
Finalmente, para asignar el material, se debe hacer doble click en el objeto del material en el panel "Model". Esto abrirá un cuadro en el que se podrá asignar el material tanto a solidos como a caras.

No se deben asignar materiales a ejes, ya que este no es soportado por el sistema y romperá al momento de la exportación del mallado y propiedades.

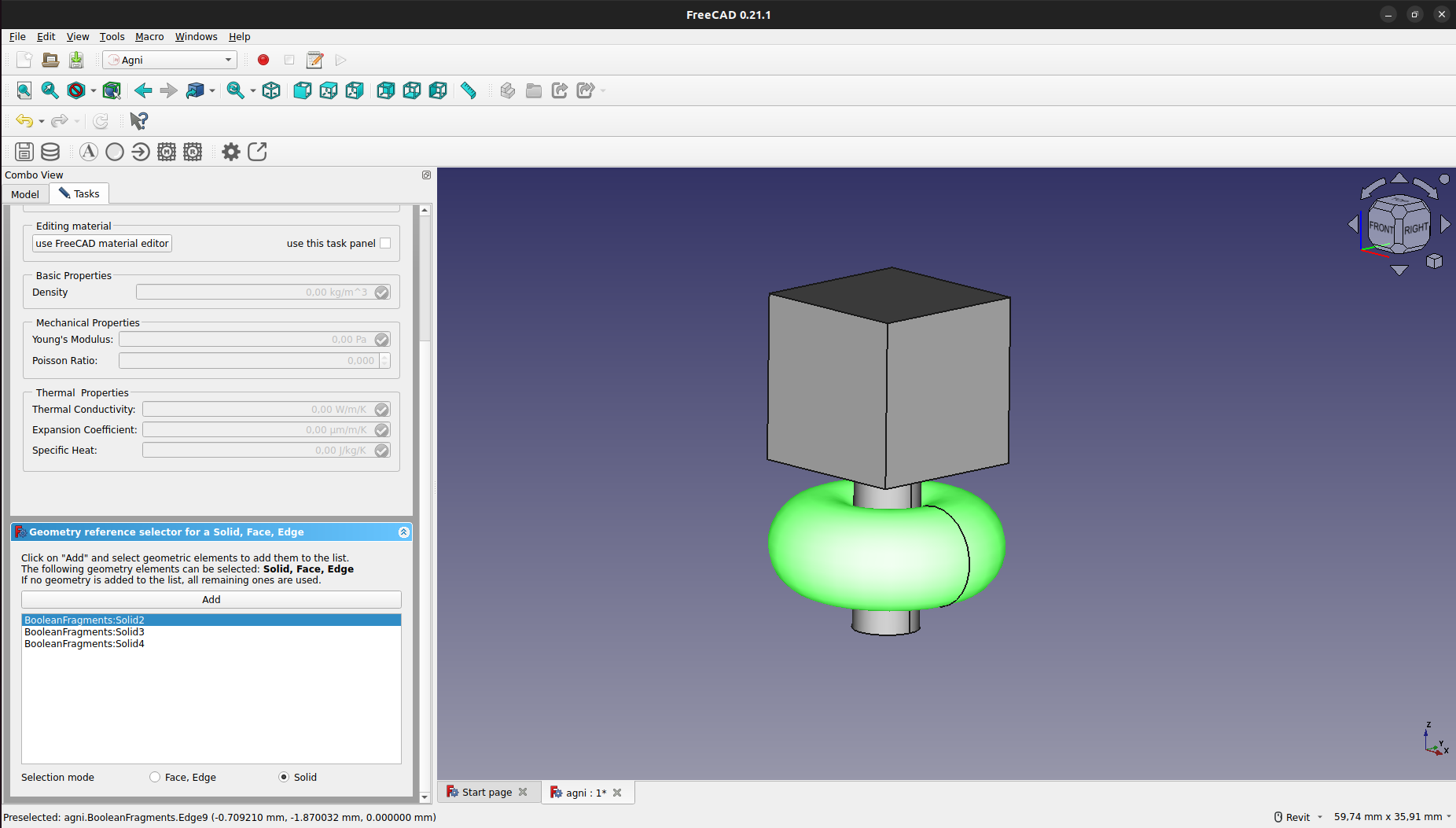
Asignación de Condiciones de Contorno

Para crear una nueva condición de contorno, se debe presionar el botón de edición de condiciones, como se muestra a continuación:

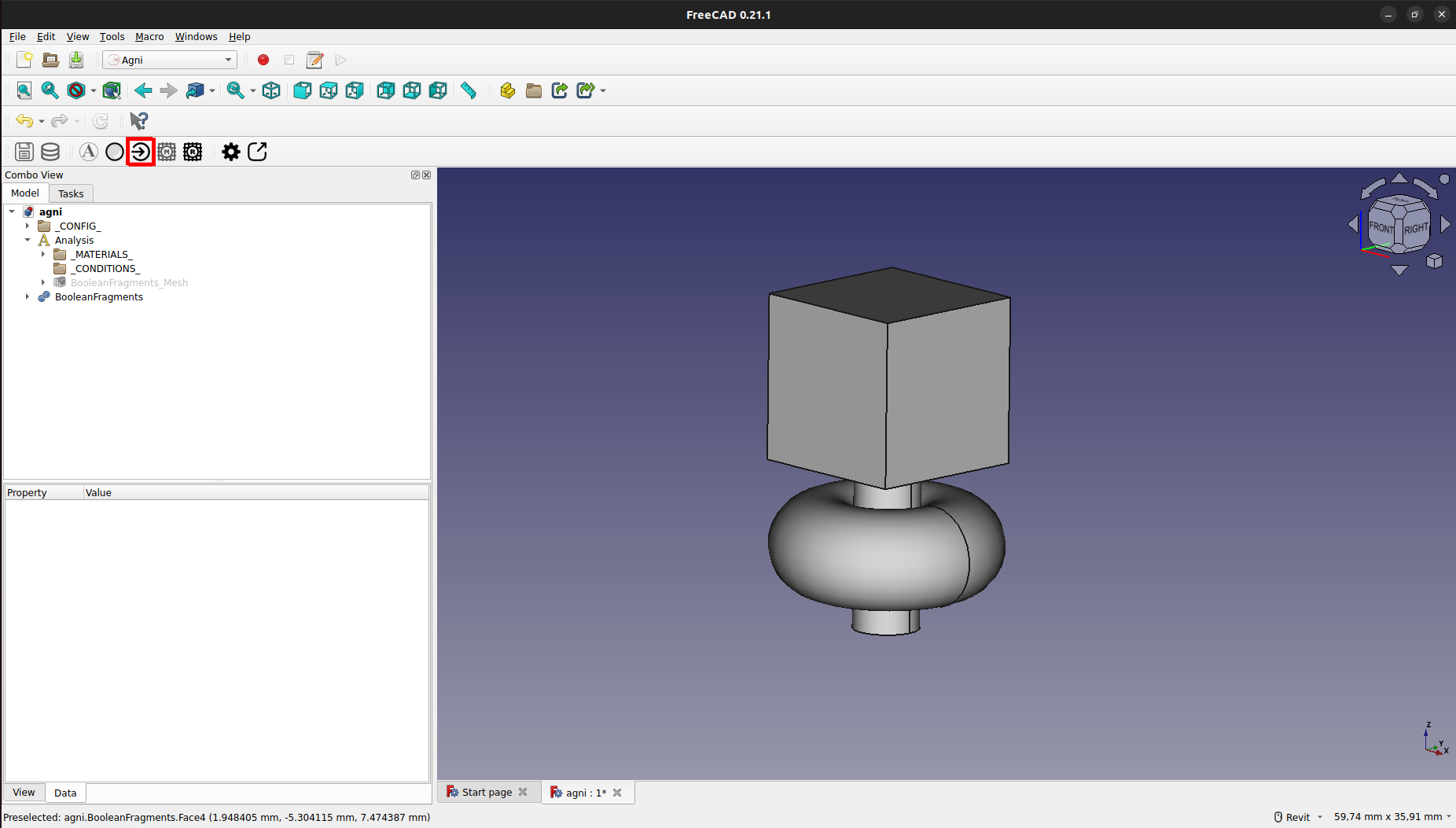
Esto abrirá una ventana con el editor de condiciones, en el cual se debe presionar "Add Condition" para agregar una nueva condición.

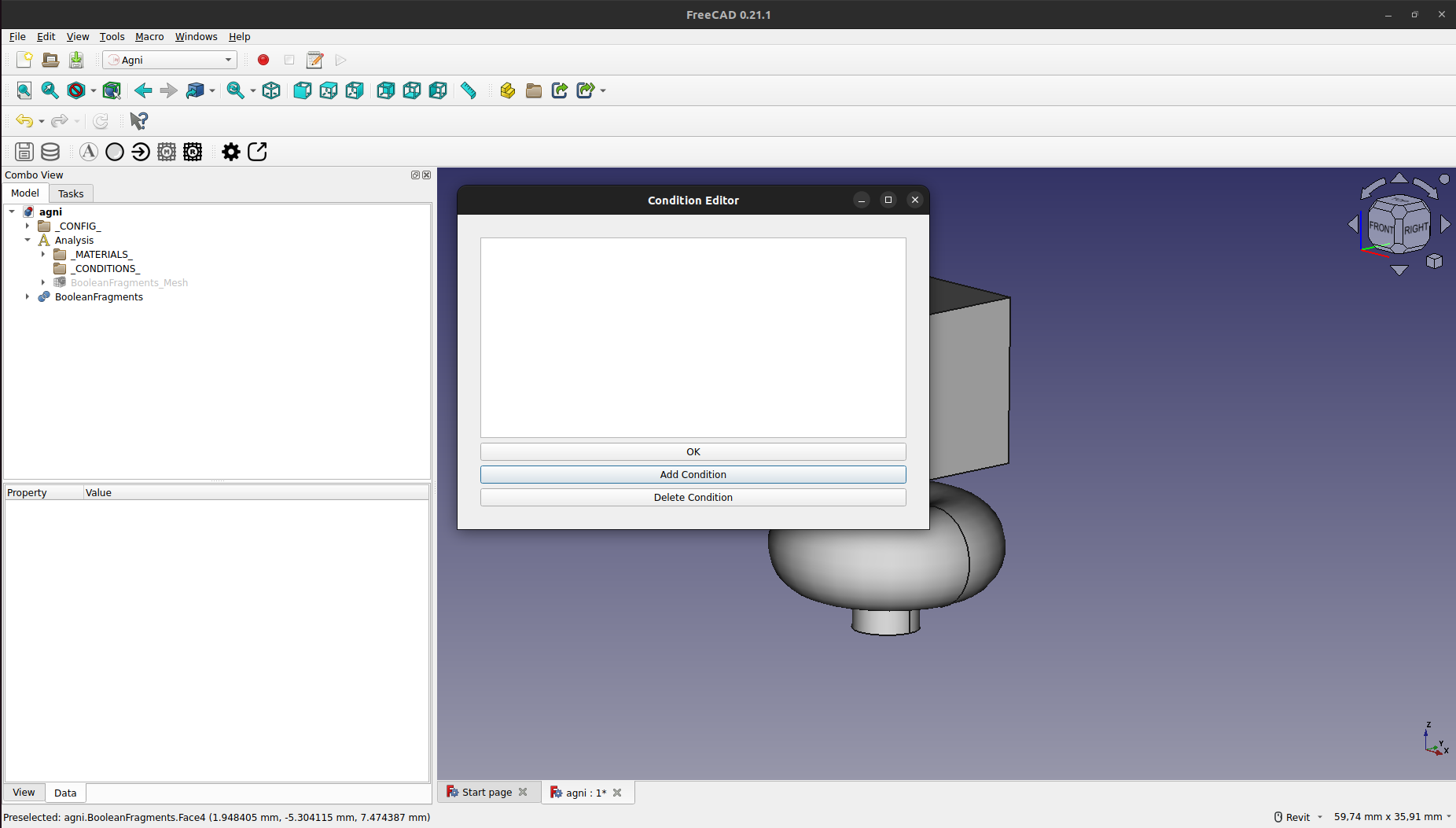
Se debe poner un nombre, "Flujo1" en este caso, y presionar "OK".

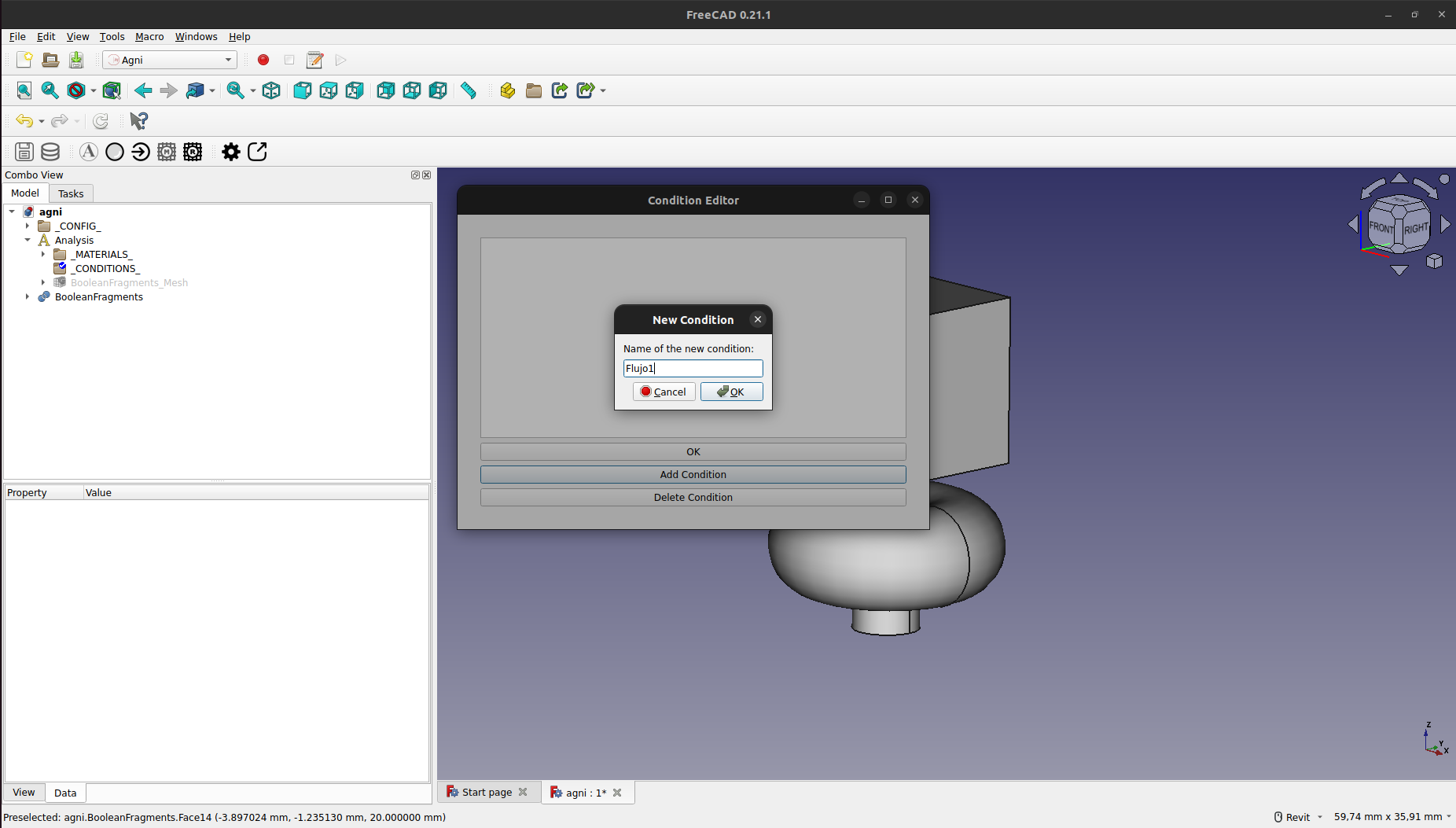
Esto creará la nueva condición, la cual se puede editar presionando sobre la misma.

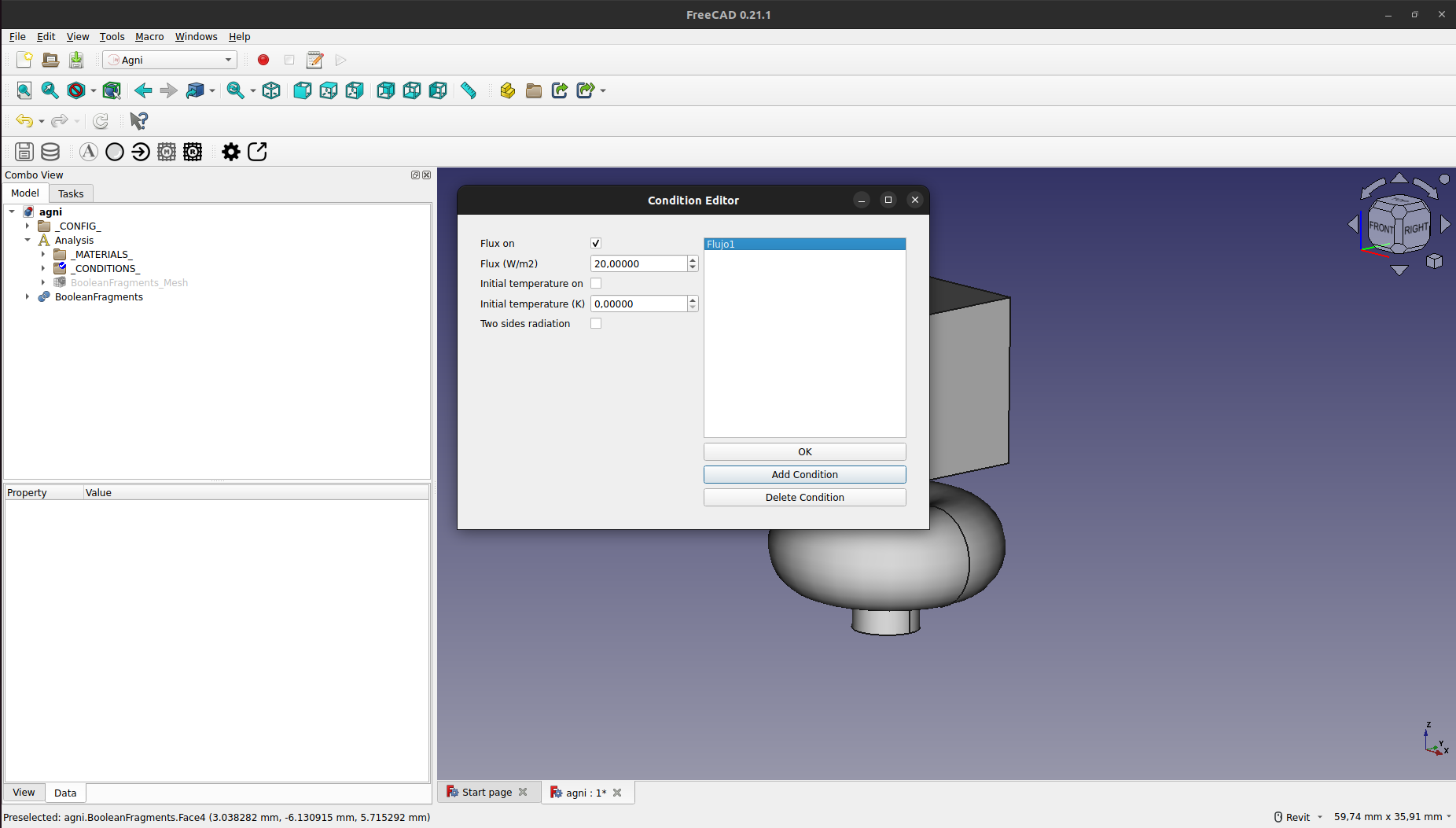
Una vez creada, aparecerá en el panel del modelado con el nombre elegido, bajo el grupo de "_CONDITIONS_"

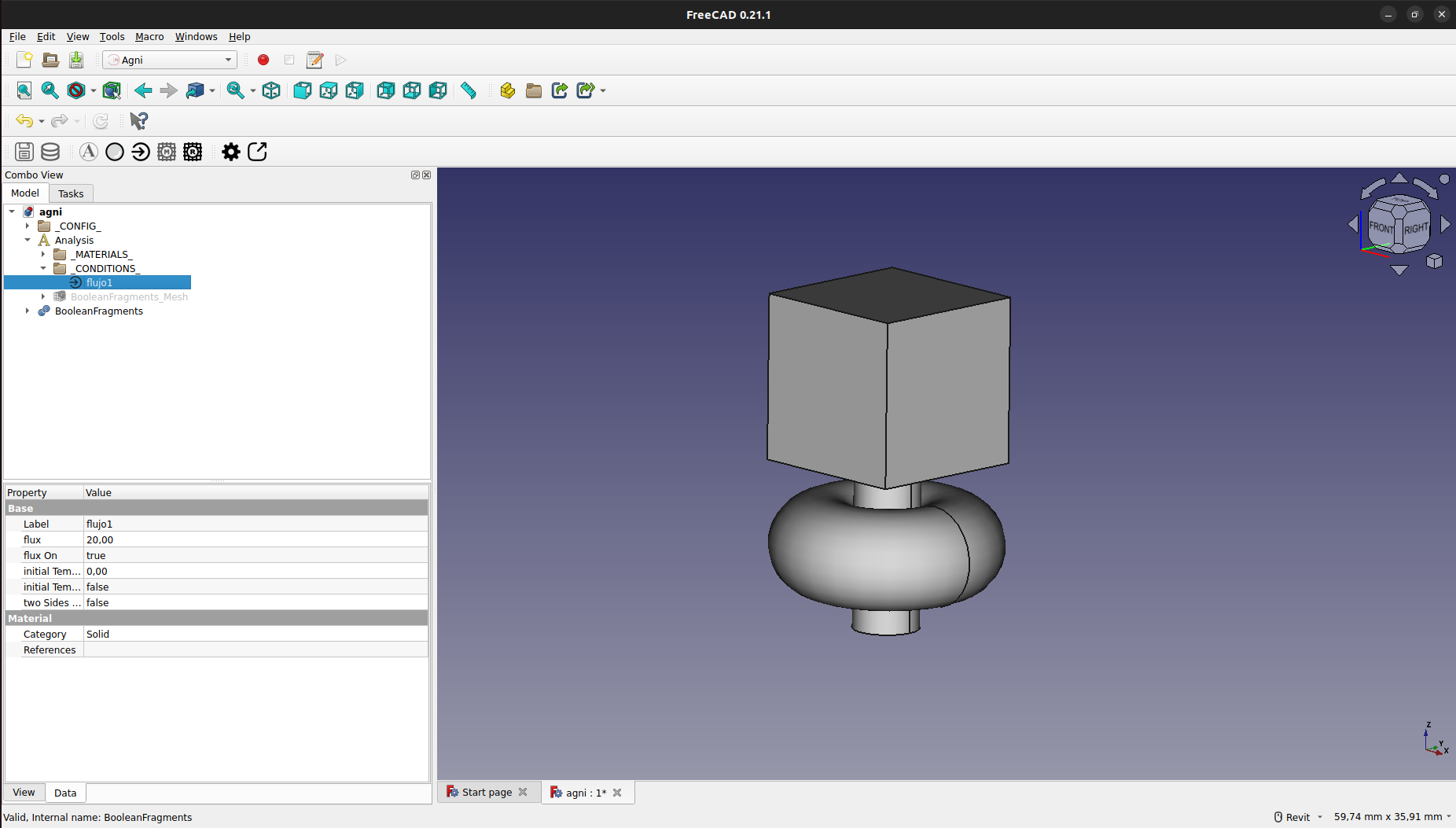
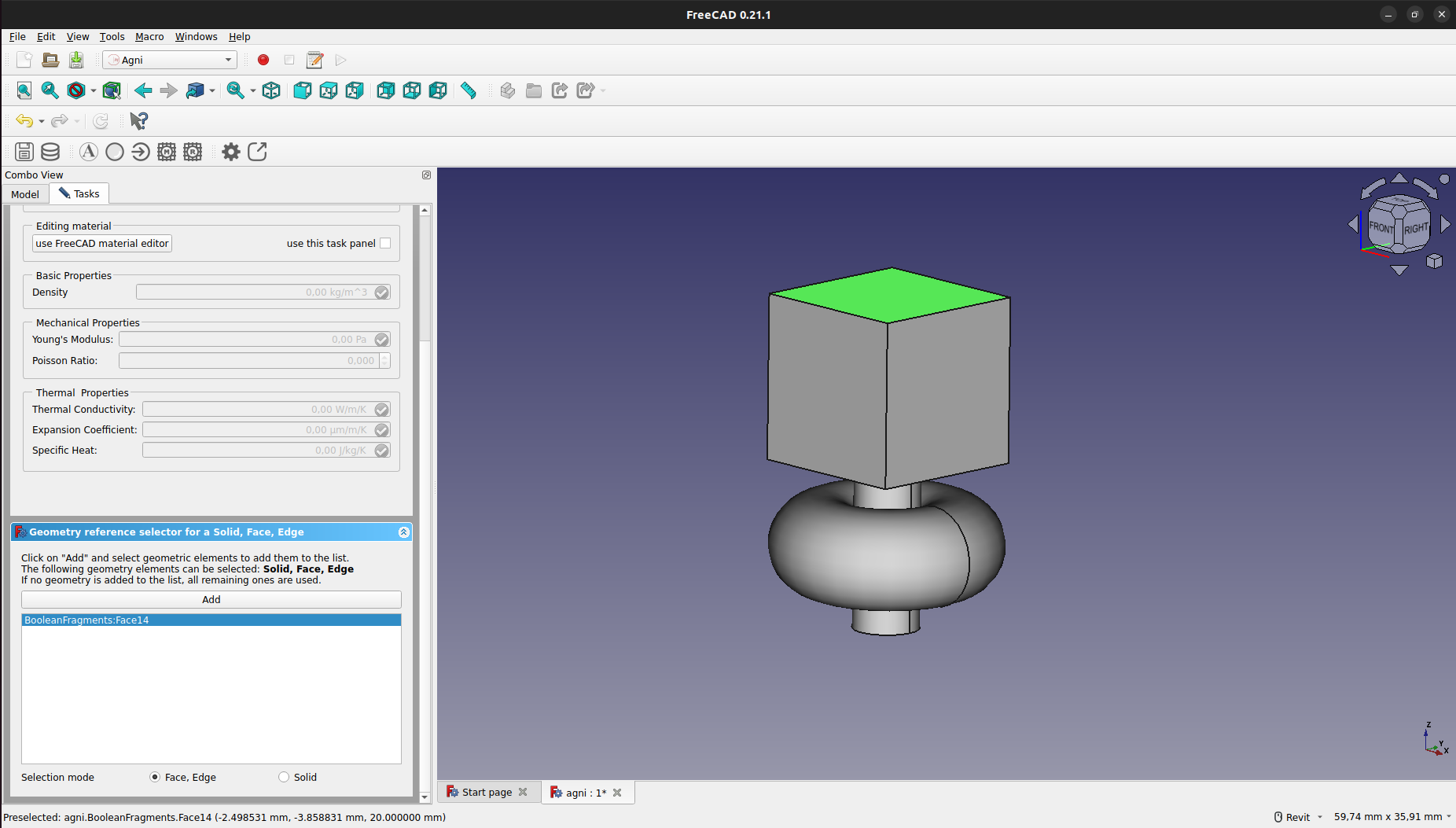
Finalmente, para asignar la condición, se debe hacer doble click en el objeto de la condición en el panel "Model". Esto abrirá un cuadro en el que se podrá asignar la condición tanto a sólidos como a caras.

No se deben asignar condiciones a ejes, ya que este no es soportado por el sistema y romperá al momento de la exportación del mallado y propiedades.

Edición de Propiedades Globales

Para editar las propiedades globales, se debe presionar el botón de edición de propiedades globales, como se muestra a continuación:

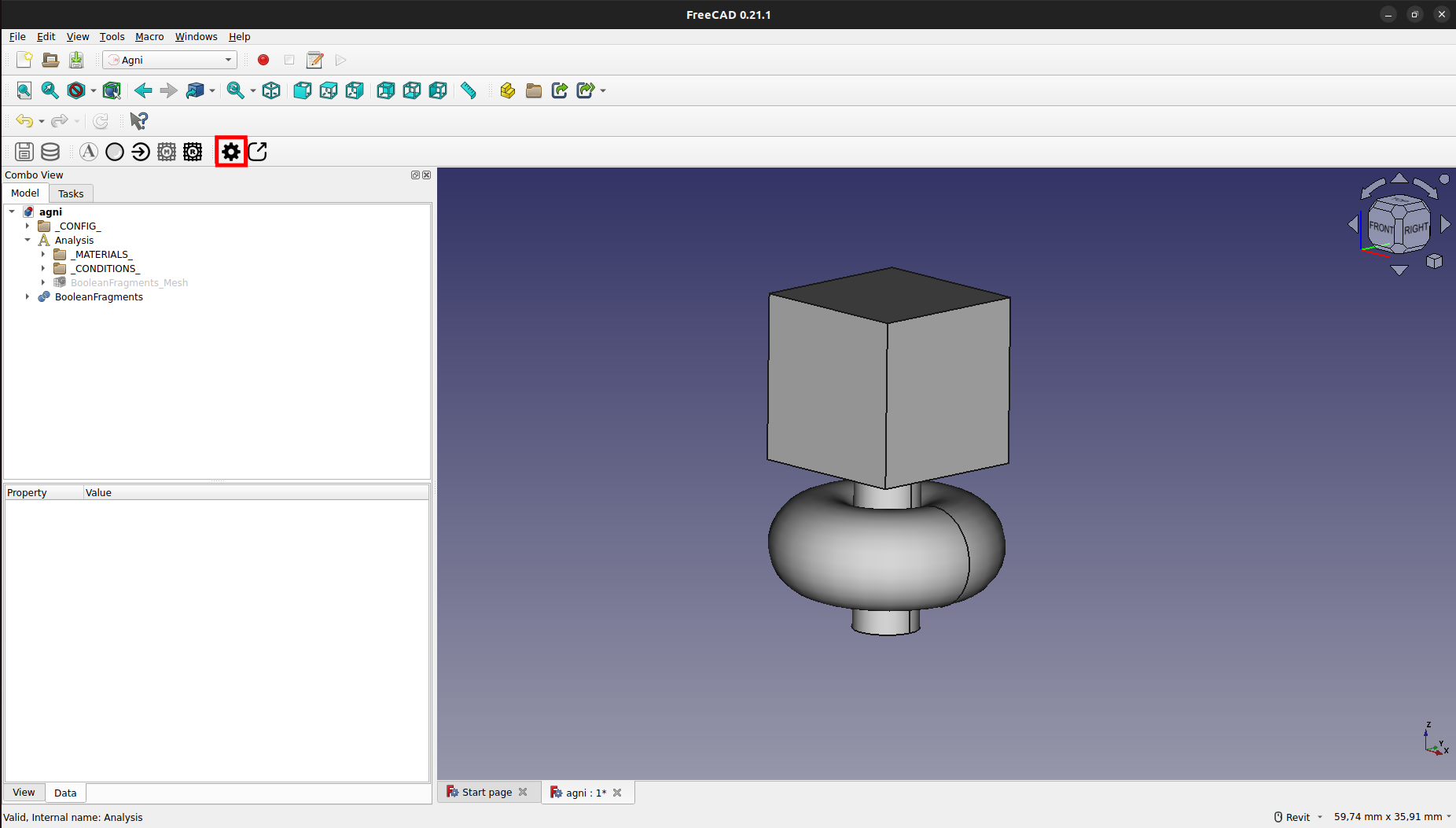
Esto abrirá una ventana con el editor de propiedades globales. Aquí se podrán editar propiedades tanto correspondiente al sistema como a la simulación en sí.

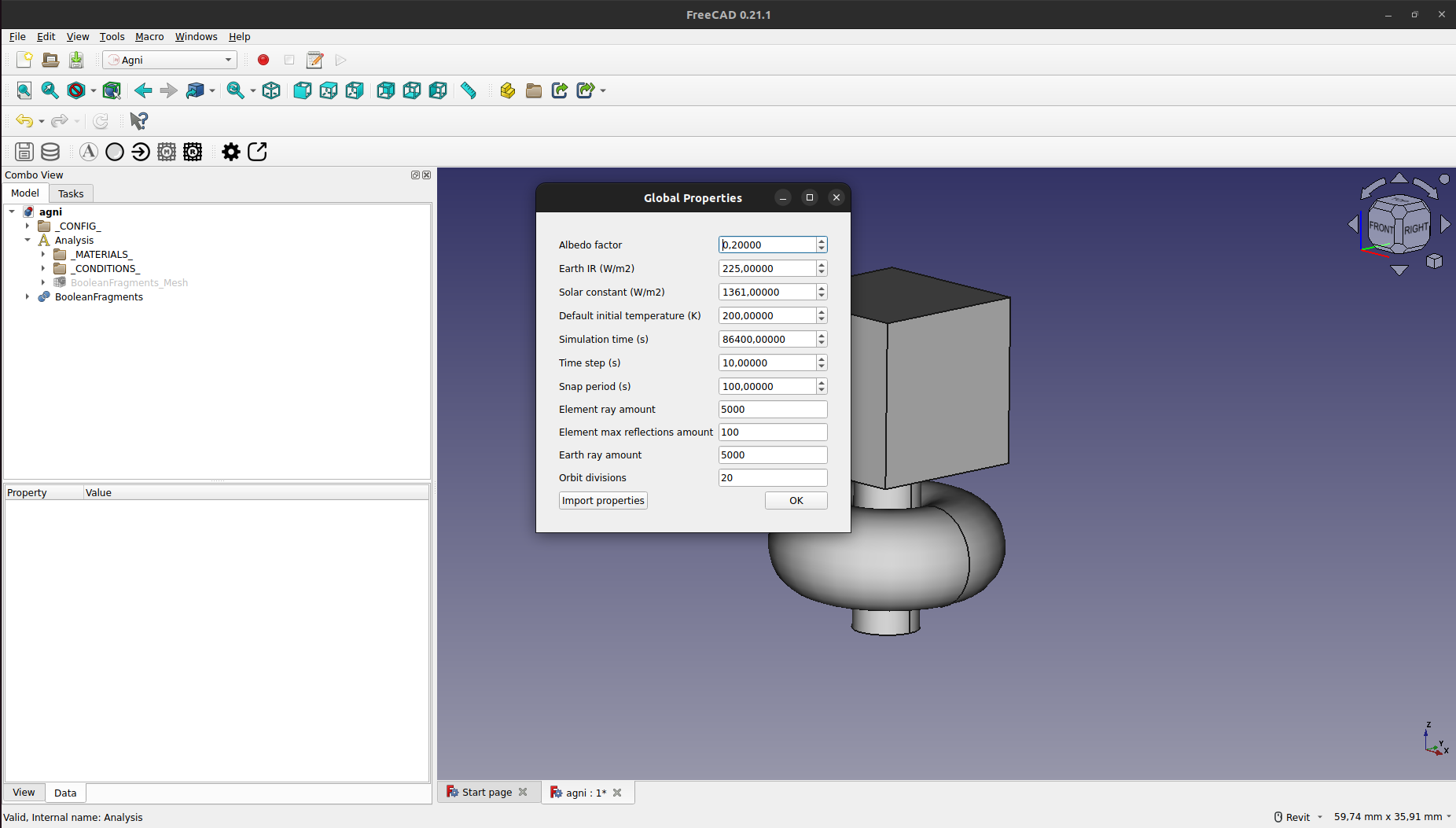
Exportación del Mallado y Propiedades

Para exportar el mallado y las propiedaes, se debe presionar el botón de exportado, como se muestra a continuación:

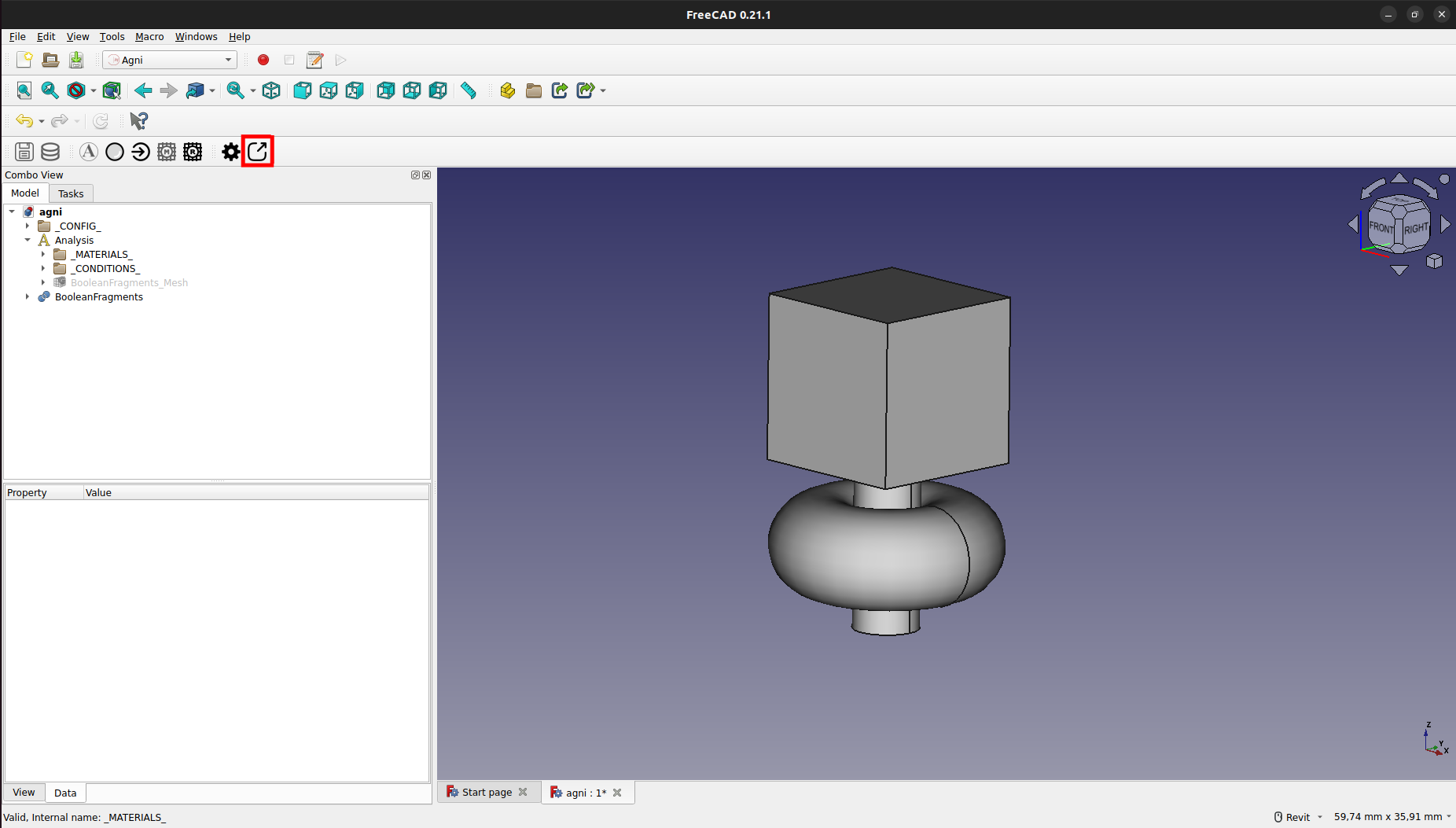
Esto abrirá una ventana para la exportación. En esta ventana se podrá editar el path de exportación, que por defecto será la ubicación del proyecto. Se recomienda no editar esta ubicación a menos que sea necesario, ya que puede traer problemas en la ejecución de los pasos siguientes.

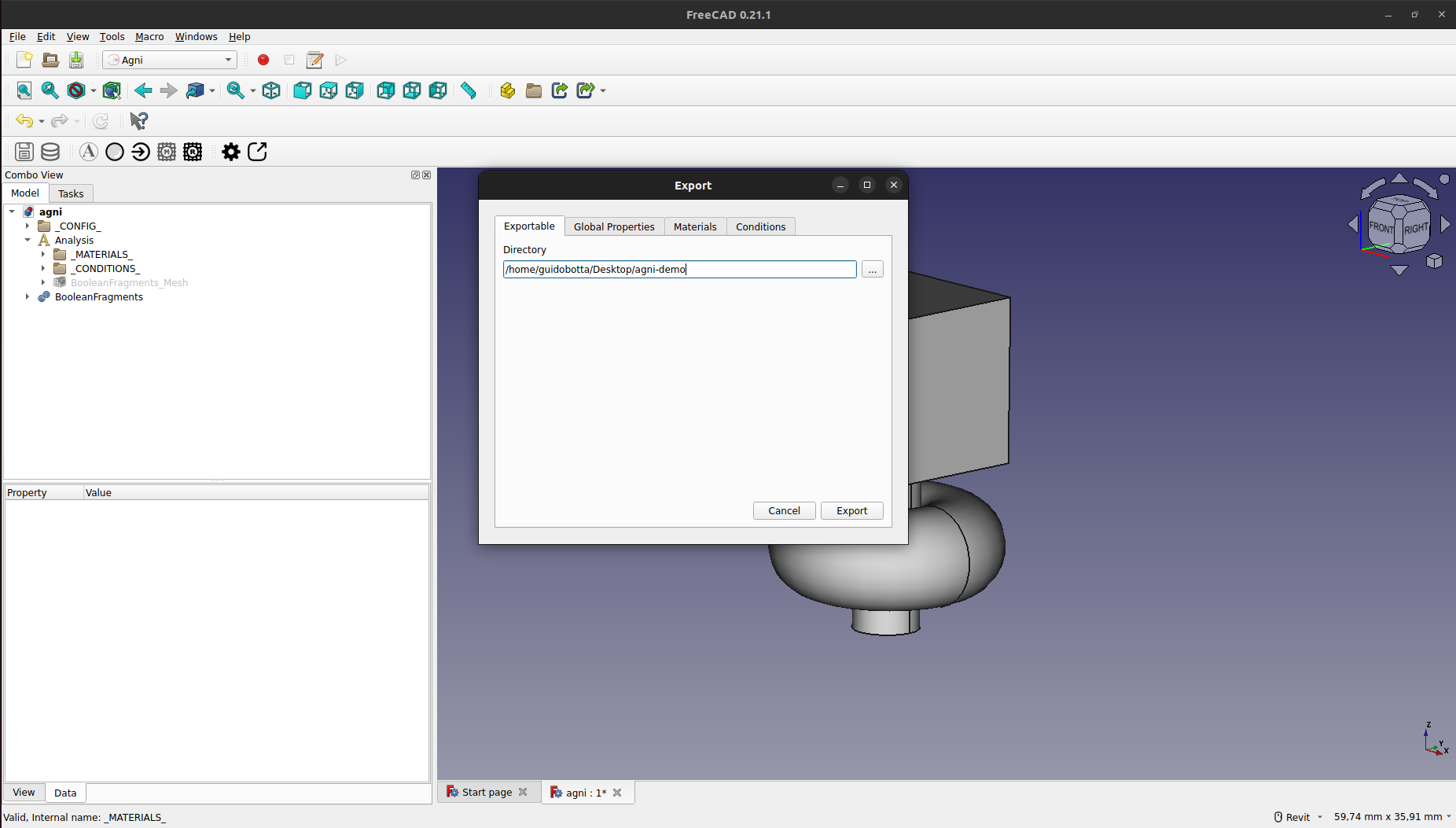
Para realizar el exportado, se debe presionar en el botón "Export". Esto generará, en el directorio seleccionado, un archivo mesh.vtk, con la representación del mallado, y un archivo properties.json, con las propiedades globales, los materiales y las condiciones de contorno.

Preprocesador

Referencia rápida

Uso general

python3 main.py <operación> <directorio>

Donde operación define las tareas a realizar y directorio es la carpeta en donde se buscarán los archivos requeridos.

Ejemplos:

python3 main.py process home/usuario/proyectos/satelite
python3 main.py process ./proyectos/satelite
python3 main.py viewm ./proyectos/satelite
python3 main.py viewn ./proyectos/satelite

Estructura de properties.json

El archivo properties.json presenta tres secciones principales "global_properties", "materials" y "conditions"

Propiedades globales

"global_properties": {
    "albedo": 0.2,
    "earth_ir": 225.0,
    "solar_constant": 1361.0,
    "initial_temperature": 200.0,
    "element_ray_amount": 5000,
    "earth_ray_amount": 5000,
    "element_max_reflections_amount": 3,
    "orbit_divisions": 15,
    "simulation_time": 86400.0,
    "time_step": 10.0,
    "snap_period": 25.0
}

"albedo": Fracción de la luz solar recibida por la Tierra que es reflejada. Escalar positivo menor a uno.
"earth_ir": Radiación infrarroja terrestre (\( \frac{W}{m^2}\)).
"solar_constant": Radiación solar (\( \frac{W}{m^2}\)).
"initial_temperature": Temperatura inicial por defecto. Puede ser sobreescrita por las condiciones (\( K \)).
"element_ray_amount" y "earth_ray_amount" establecen la cantidad de rayos a utilizar por elemento para radiación elemento-elemento y elemento-tierra (albedo e ir), respectivamente.
"element_max_reflection_amount" es el límite de reflexiones en radiación elemento a elemento.
"orbit_divisions" establece la cantidad de puntos de la órbita a considerar, aunque es posible que se tomen menos puntos si los puntos de referencia que calcula GMAT se encuentran muy concentrados en algunas secciones.
"simulation_time": Tiempo total a simular (\( s \)).
"time_step": Intervalo de discretización. Valores más pequeños aumentan la presición, a costa de aumentar el tiempo de cálculo total (\( s \)).
"snap_period": Intervalo de muestreo de resultados. El tiempo total debe ser múltiplo de él (\( s \)).

Materiales

"materials": {
    "properties": {
        "materialA": {
            "thermal_conductivity": 0.0,
            "specific_heat": 900.0,
            "density": 2700.0,
            "thickness": 0.05,
            "alpha_sun": 1.0,
            "alpha_ir": 1.0,
       }
       "materialB": { ... }
    },
    "elements": {
        "materialA": [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
        "materialB": [12, 13, 14, 15, 16, 17, 18, 19]
    }
}

Se divide en dos subsecciones, siendo la primera "properties", en donde se especifican las caracteristicas físicas de los materiales y la segunda "elements", en donde se indica a través de un arreglo a qué elementos corresponden dichos materiales.

Las propiedades de los materiales son:

"thermal_conductivity": Conductividad térmica (\( \frac{W}{m . K}\)).
"specific_heat": Calor específico (\( \frac{J}{kg . K}\)).
"density": Densidad (\( \frac{kg}{m^3}\)).
"thickness": Grosor (\(m\)).
"alpha_sun": Absortividad en frecuencias del espectro solar. Escalar positivo menor a uno.
"alpha_ir": Absortividad en el espectro infrarojo. Escalar positivo menor a uno.

Conditions

"conditions": {
    "properties": {
        "conditionA": {
            "flux_on": true,
            "flux": 100.0,
            "initial_temperature_on": true,
            "initial_temperature": 273.15,
            "two_sides_radiation": true
            "flux": 10.0
       }
    },
    "elements": {
        "conditionA": [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
    }
}

Se divide en dos subsecciones, siendo la primera "properties", en donde se especifican las características de las condiciones y la segunda "elements", en donde se indica a través de un arreglo a qué elementos corresponden dichas condiciones.

Las características de una condición son:

"flux_on": Considerar valor de flujo inicidente. Booleano.
"flux": Flujo constante incidente (\( \frac{W}{m^2}\)).
"initial_temperature_on": Considerar valor de temperatura inicial. Booleano.
"initial_temperature": Temperatura inicial del elemento(\(K\)).
"two_sides_radiation": Indica si debe considerarse la orientación del elemento (dirección de su normal según la regla de la mano derecha) al proyectar rayos elemento a elemento.

Procesamiento de factores de vista

Archivos necesarios: mesh.vtk, properties.json, ReportFile.txt, EclipseLocator.txt

Calcula factores de vista entre elementos del satélite, Tierra y el Sol.

Ejecución de ejemplo de operación process

Almacena los resultados en un archivo binario view_factors.vf.

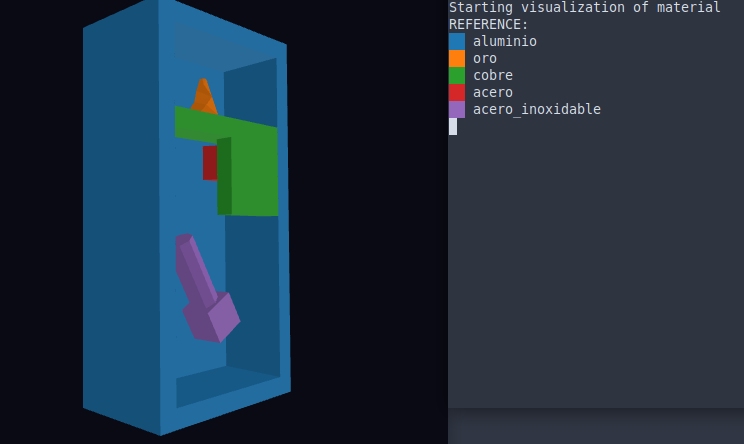
Visualización de materiales

Archivos necesarios: mesh.vtk, properties.json

Muestra en tres dimensiones los materiales asignados a cada elemento sobre el modelo.

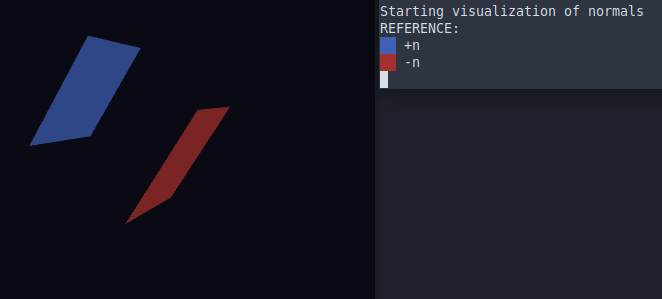
Ejecución de ejemplo de operación viewm

Visualización de orientación de normales

Archivos necesarios: mesh.vtk

Muestra en tres dimensiones la orientación (dirección de la normal) de cada elemento sobre el modelo.

Ejecución de ejemplo de operación viewn

Solver

Ejecución

En caso de querer ejecutar el Solver por fuera de la GUI, se debe ejecutar el siguiente comando:

./target/release/solver <directory> <method>

Siendo <directory> el directorio donde se encuentran los archivos necesarios, mientras que <method> debe tomar el valor de "Implicit" o el de "GPU"

Los archivos necesarios para ejecutar el solver son: mesh.vtk, properties.json y view_factors.vf.

Una vez ejecutado, genera una carpeta results que contiene un archivo result.vtk.series y un archivo result<i>.vtk por cada instante de la simulación.

Parámetros

Los parámetros necesarios para ejecutar el solver que se encuentran en el properties.json son los siguientes:

Global Properties

"global_properties": {
    "orbital_period": 5828.516639879384,
    "albedo": 0.2,
    "earth_ir": 225.0,
    "solar_constant": 1361.0,
    "initial_temperature": 293.15,
    "simulation_time": 175000.0,
    "time_step": 10.0,
    "snap_period": 100.0,
    "orbit_divisions": 60,
    "eclipse_start": 603.2083601206168,
    "eclipse_end": 2646.8503601206166
}

"orbital_period": Indica el periodo de la orbita, es generado por el preprocesador.
"albedo": Factor de albedo.
"earth_ir": Flujo de calor proveniente por la radiación IR de la tierra \([\frac{W}{m^2}]\).
"solar_constant": Constante de flujo solar \([\frac{W}{m^2}]\).
"simulation_time": Tiempo de simulación expresado en segundos.
"time_step": Paso de tiempo que usara la simulación, esta expresado en segundos.
"snap_perior": Indica cada cuanto tiempo se guardara un resultado, esta expresado en segundos.
"orbit_divisions": Cantidad de divisiones en la orbita para los factores de vista.
"eclipse_start": Indica cuando empieza el eclipse, es generado por el preprocesador.
"eclipse_end": Indica cuando termina el eclipse, es generado por el preprocesador.

Los parámetros "albedo", "earth_ir", "solar_constant", "initial_temperature", "simulation_time", "time_step" y "snap_period" pueden ser alterados manualmente para modificar las caracteristicas de la simulación sin necesidad de volver a ejecutar el preprocesador, lo que disminuye el tiempo total empleado. Una modificación en cualquiera de los parámetros restantes requiere volver a ejecutar el preprocesador para el correcto funcionamiento de la simulación.

Materials

"materials": {
    "properties": {
        "aluminio": {
            "thermal_conductivity": 237.0,
            "specific_heat": 900.0,
            "density": 2700.0,
            "thickness": 0.05,
            "alpha_sun": 1.0,
            "alpha_ir": 1.0,
            "name": "aluminio"
        }
    },
    "elements": {
        "aluminio": [1,2,3,4,5,6,7,8]
    }
}

Las propiedades de los materiales son:

"thermal_conductivity": Conductividad térmica \([\frac{W}{m \ K}]\).
"specific_heat": Calor específico \([\frac{J}{kg \ K}]\).
"density": Densidad \([\frac{kg}{m^3}]\).
"thickness": Grosor \([m]\).
"alpha_sun": Absortividad en frecuencias del espectro solar. Escalar positivo menor a uno.
"alpha_ir": Absortividad en el espectro infrarojo. Escalar positivo menor a uno.

Los parámetros "thermal_conductivity", "specific_heat", "density" y "thickness" pueden ser alterados manualmente sin necesidad de volver a ejecutar el preprocesador.

Conditions

"conditions": {
    "elements": {
        "hot_temperature": [
            1,2,3,4
        ]
    },
    "properties": {
        "hot_temperature": {
            "initial_temperature_on": true,
            "initial_temperature": 573.0,
            "flux_on": false,
            "flux": 0.0,
            "two_sides_radiation": false
        }
    }
}

Las características de una condición son:

"flux_on": Indica si se debe considerar el valor del parametro "flux"
"flux": Flujo constante incidente (\(\frac{W}{m^2}\)).
"initial_temperature_on": Indica si se debe considerar el valor del parametro "initital_temperature"
"initial_temperature": Temperatura inicial (\(W\)).
"two_sides_radiation": Indica si los elementos emiten radiación hacia ambos lados.

Los parámetros "flux_on", "flux", "initial_temperature_on" e "initial_temperature" pueden ser alterados manualmente sin necesidad de volver a ejecutar el preprocesador.

Tiempo de ejecución vs Precisión

La modificación de los distintos parámetros implica, en general, un tradeoff entre el tiempo de ejecución y precisión. Aquellos parámetros que tienen impácto en alguna de estas dos variables son:

"simulation_time": Al aumentar, incrementa el tiempo de ejecución.
"time_step": Al disminuir, mejora la precisión de la simulación, a costa de un mayor tiempo de ejecución.
"snap_period": Al disminuir, mejor será la resolución de datos extraidos de la simulación, a costa de un mayor tiempo de ejecución.
"orbit_divisions": Al aumentar, mejor será la discretización de la órbita y con ello la precisión de la simulación, a costa de un mayor tiempo de ejecución.
Cantidad de elementos en malla: Al aumentar, mejor será la discretización del modelo y con ello la precisión de la simulación, a costa de un mayor tiempo de ejecución.

Paraview

En este manual se describirán los pasos básicos a seguir para poder visualizar los resultados de la simulación en el software Paraview, se recomienda al usuario utilizar documentación externa en caso de querer hacer uso de funcionalidades mas complejas.

Comenzando en la pantalla principal de Paraview

Importación de resultados

Haciendo click en File -> Open

O bien click derecho dentro del recuadro Pipeline Browser

Se abrirá una ventana en la cuál podrán buscar los archivos de resultados, una vez en la carpeta donde estos se encuentran, se debera seleccionar el archivo *.vtk.series

Esto añadira al Pipeline Browser el archivo con los resultados

Para que estos sean visibles se debe hacer click en el boton con forma de ojo a la izquierda del nombre

Una vez hecho esto se podrán visualizar los resultados

Visualización a lo largo del tiempo

Para poder visualizar las temperaturas a lo largo del tiempo se debe ir al panel "View" y activar la opción "Time Manager"

Esto abrirá el siguiente panel

En este se podrá elegir que instante de tiempo se quiere visualizar

Cabe aclarar que el rango de temperaturas a visualizar se mantiene constante cuando se cambia de instante, por lo que en casos en que los cambios de temperatura sean muy grandes, no se percibirán correctamente los resultados, para solventar esto, una vez seleccionado el instante que se quiere visualizar se debe hacer click en el siguiente boton para ajustar el rango de temperatura, el cual setea el minimo y el maximo correspondientes a las temperaturas de este instante

Se puede observar a continuación un ejemplo de como cambia el rango de temperaturas luego de clickear este boton

Herramiente de Querys

Se recomienda el uso del siguiente panel para realizar consultas especificas sobre los datos. Se debe ir al panel "View" y activar la opción "Find Data"

El cual abre el siguiente panel

Se debe seleccionar en "Data Producer" el archov *.vtk.series

En la primera parte se pueden seleccionar los criterios de busqueda, como si se va a buscar sobre puntos o celdas.

En caso de buscar sobre puntos, se puede realizar la consulta sobre ID, Temperatura o Point (posicion x,y,z)

Luego se puede elegir la condición de busqueda y ingresar el valor

Al hacer presionar "Find Data" se realiza la busqueda

Esto generará puntos rosas sobre el modelo que indican que nodos cumplen con la condicion dada

Si se activa la siguiente opción, se podrá visualizar sobre cada nodo su ID o Temperatura

Se debe tener en cuenta que si la consulta genera muchos resultados no todos los nodos mostrarán su ID, por lo que en caso de querer saber el ID de un nodo especifico se debe hacer una consulta que devuelva poca cantidad de nodos.

Plotter

Ejecución

En caso de desear ejecutar el Plotter por fuera de la GUI, se debe ejecutar el siguiente comando:

python3 UI.py

Uso del Plotter

La interfaz de usuario del Plotter corresponde con lo que se muestra en la siguiente captura:

Para cargar los datos de la simulación será necesario presionar el botón "Choose File". Esto abrirá una nueva ventana en la cual se podrá seleccionar el archivo *.vtk.series deseado.

El tiempo de carga de los resultados dependerá del tamaño del modelo y la cantidad de archivos generados.

Tras finalizar la carga se indicará el path del archivo procesado.

Existen 4 graficos distintos que se pueden seleccionar. El primero, "All Temperatures Over Time" muestra un grafico de la temperatura en relacion al tiempo con una linea para cada nodo.

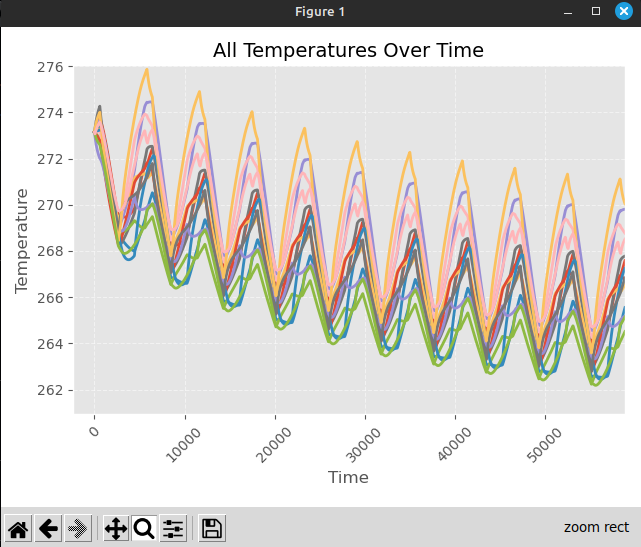
El segundo, "Temperature Over Time" permite visualizar la temperatura de un solo nodo a elección, para lo cuál se debe indicar su ID. Referirse al manual de Paraview para obtener el ID de un nodo.

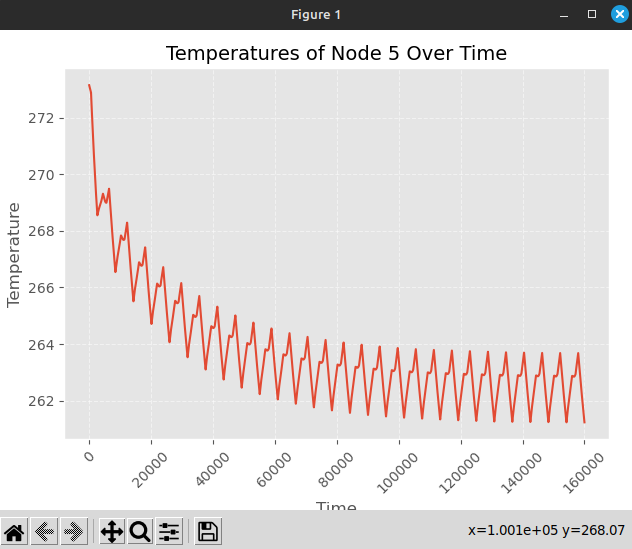
El tercero, "Average Temperature Over Time" muestra la temperatura promedio de los nodos a través del tiempo.

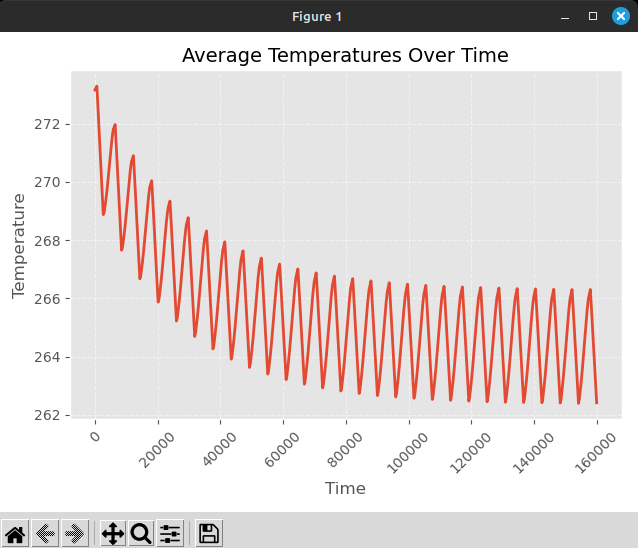
El cuarto, "Standard Deviation Over Time" muestra la desviación estándar de la temperatura de los nodos a través del tiempo.

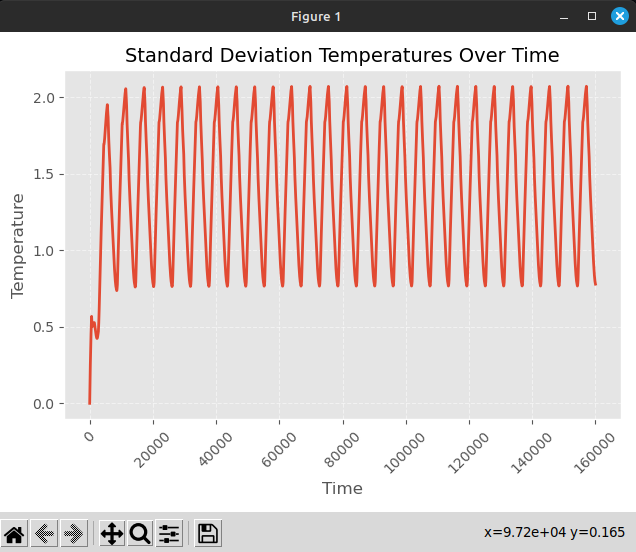
Manual Técnico

En el manual técnico se tratarán los siguientes temas:

Mallado

Agni B3V utiliza un mallado FEM como representación numérica del modelo satelital a lo largo de la simulación térmica.

En un mallado FEM, la estructura de un cuerpo se construye a partir de elementos. En dos dimensiones pueden utilizarse triángulos o cuadriláteros, mientras que para tres dimensiones tetraedros y hexaedros son una elección habitual.

A esto se le suma la posibilidad de utilizar elementos de distinto orden. Un mayor orden en los elementos permite una mayor deformación del mallado a lo largo del tiempo de la simulación. Este punto no es de particular interés en la simulación térmica satelital cuando se trabaja entre rangos de temperatura donde la estructura no se deforma significativamente. Además, un mayor orden en el mallado implica un mayor costo computacional.

Es importante que un mallado FEM sea bueno para no introducir mayor error numérico. Para ello, hay ciertos puntos a tener en cuenta:

Las transiciones de densidades de elementos en la malla no deben ser abruptas.
Las transiciones de densidad de elementos deben estar localizadas lejos de las regiones de mayor interés.
Es recomendable no tener grandes diferencias entre los elementos de menor y mayor tamaño. Sobre todo si son regiones cercanas.

Órdenes en un elemento triángular bidimensional

Modelo FEM en Agni B3V

En Agni se utiliza un mallado bidimensional, triangular y de primer orden. Se genera utilizando el mallador Gmsh que se encuentra integrado en FreeCAD. Se hablará con más detalle sobre el modelo numérico en la sección de Modelo FEM.

A continuación se puede ver un ejemplo concreto de un mallado realizado en FreeCAD:

La generación del mallado se puede ver con mayor detalle en la sección de Agni Addon.

Preprocesador

El preprocesador fue ideado como un breve script de python para adaptar archivos disímiles a un formato legible por el solver y acabó cubriendo todo lo referido al cálculo de factores de vista.

La malla tridimensional del satélite, junto con los materiales asignados a cada polígono que la compone, son información suficiente para el cálculo de la transmisión de calor por conducción. Estos datos ya se encuentran estructurados de forma tal que es preciso y eficiente considerar solo el aporte de calor de la vecindad para cualquier punto en un tiempo determinado.

En cambio, para la transmisión de calor por radiación, la energía recibida en un punto es el resultado de integrar los rayos que fueron emitidos/reflejados por otros cuerpos (Tierra, Sol) u elementos del mismo satélite. Pese a ello, en el dominio del problema, ni la geometría del satélite, ni las características de los materiales se modifican. Más aún, los rayos viajan por el vacío, con lo que su energía solo disminuye con los rebotes. Estas simplificaciones permiten transformar la integración del efecto de rayos individuales en flujos constantes de energía en función de factores de vista entre elementos y los astros. De forma tal que conducción y radiación puedan resolverse homogéneamente con operaciones matriciales en el solver. Como ventaja adicional, la magnitud del aporte energético se separa de la proporción que se esperaría que un cuerpo reciba de otro, permitiendo reutilizar parámetros geométricos en distintos escenarios físicos.

El factor de vista es un concepto central en muchos de los modelos de cálculo de radiación y puede entenderse coloquialmente como la proporción del campo de vista que cubre una superficie respecto a otra.

El método Monte Carlo permite definir y aproximar factores de vista con mayor precisión. En él se seleccionan puntos del elemento emisor y direcciones al azar en la que se emiten rayos, se toma registro de los elementos impactados y luego se computa el factor de vista como la razón entre los rayos impactados y el total de rayos emitidos. Dependiendo del propósito de la simulación, se pueden emitir rayos desde un elemento en todas las direcciones, como si fuese una placa, o solo en dirección de la normal, suponiendo que es parte de un cuerpo sólido. También pueden introducirse reflexiones reemitiendo rayos desde las posiciones de impacto.

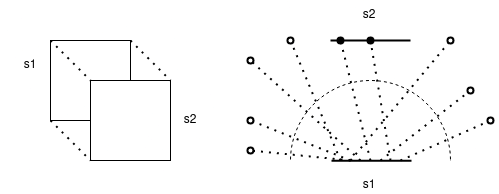
En el ejemplo de la figura se disparan diez rayos desde \(s1\), de los cuales solo dos impactan \(s2\), por lo que el factor de vista entre \(s1\) y \(s2\) se aproximaría como \(\frac{2}{10}\). Notar que si \(s1\) y \(s2\) no tuviesen la misma área, el factor de vista \(s1s2\) diferiría del factor de vista \(s2s1\). Si se tratasen de dos cuerpos negros, la energía que \(s1\) aporta a \(s2\) podría calcularse como el producto entre el total de energía emitida por \(s1\) y el factor de vista \(s1s2\).

Para introducir el efecto de los materiales sobre la reflexión se evaluaron dos enfoques:

Enfoque A: Considerar la pérdida de energía por rayo en cada rebote de acuerdo con las características del material y desaparecer al no sobrepasar un nivel de energía despreciable cutoff.
Enfoque B: Utilizar números pseudoaleatorios para decidir si un elemento absorbe o no a un rayo y solo contar al elemento que finalmente lo absorbió.

Se optó por el enfoque B, dado que si bien el enfoque A producía resultados más precisos para pocos rayos, acababa por disparar mayor cantidad de rayos al ser más frecuentes las reflexiones. Además, fue más sencillo pensar el efecto de los materiales sobre rayos individuales.

En las siguientes secciones se especifica la implementación de cada interacción en la que se descompone el cálculo de transmisión de calor por radiación.

Interacción Elemento-Sol

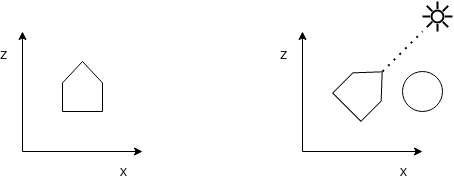
Dada la distancia promedio entre el satélite y el Sol, los rayos que éste emite e impactan al satélite lo hacen en un ángulo comparable, es decir, el satélite interactúa con el Sol como si se tratase de un conjunto de rayos paralelos. Además, en una órbita de tipo "Sun pointing" la aptitud del satélite no se modificará de forma apreciable. Aun así, fue necesario rotar el modelo del satélite para alinearlo con el Sol al inicio de la simulación. Para ello, se definió que se modele el mismo tomando al eje Z en sintido positivo como la dirección hacia el Sol.

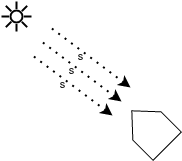
Fue posible simplificar aún más la estimación de las zonas iluminadas. En vez de emitir rayos desde el plano definido por la dirección del Sol, esperando que se alcancen todos los elementos del satélite, pueden emitirse rayos desde los elementos hacia el Sol. Si un rayo colisiona con el propio satélite, el rayo inverso Sol-satélite también colisionará (aunque no necesariamente con el mismo punto), mientras que de perderse el rayo en el espacio, necesariamente el rayo inverso podría llegar al elemento sin problemas.

Por último, se debió aplicar una corrección de intensidad de las áreas iluminadas por el área aparente, lo que está implícito en el método Monte Carlo al promediar la colisión de múltiples rayos. En la figura observamos el caso bidimensional en donde la longitud del elemento es L, pero debido al ángulo de su normal respecto a la dirección de incidencia de los rayos solares, la proporción de radiación que recibe es menor:

\[ P = L \sin({\theta} _l) \]

\[ \theta_n = \theta _l + \frac{\pi}{2} \]

\[ \theta_{sn} = \pi - \theta_n = \frac{\pi}{2} - \theta _l \]

Entonces:

\[ P = L \sin(\frac{\pi}{2} - \theta_{sn}) = L \cos(\theta_{sn}) \]

Al utilizar elementos con vértices coplanares para el mallado (en nuestro caso triángulos), este razonamiento puede extenderse directamente al caso tridimensional.

Interacción Elemento-Elemento

Para llevar cuenta de los factores de vista elemento a elemento se inicializa una matriz cuadrada con la misma cantidad de filas y columnas que de elementos. Los factores de vista no son simétricos, por lo que no se puede ahorrar cómputo o espacio en memoria con matrices triangulares.

Se emite la misma cantidad de rayos desde cada elemento y para cada rayo que colisionó se genera un número pseudoaleatorio entre cero y uno y se lo compara con la absortividad al espectro infrarrojo del material del elemento impactado. Si es menor, se suma uno a la fila del elemento emisor y la columna del elemento impactado. De lo contrario, se reemite el rayo desde la posición de la colisión en la dirección reflejada respecto a la normal del elemento. Tras considerar todos los rayos de un elemento, se divide la fila correspondiente por el total de rayos emitidos. Se introdujo un límite de reflexiones consideradas para asegurar que el algoritmo finalice en tiempo finito, aunque gracias a esto es posible que una fracción de rayos se pierdan cuando en la realidad no sería así.

Notar que los factores de vista elemento a elemento solo dependen de la geometría del modelo del satélite y, por tanto, alcanza con calcularlos una única vez.

Interacción Elemento-Tierra

Debido a la poca distancia que los separa, el satélite interactúa con la Tierra como si de un plano infinito se tratase. Los rayos provenientes de la Tierra por radiación infrarroja o albedo (reflejo de la luz solar) son emitidos desde puntos dentro del plano y direcciones aleatorias. El inconveniente con ceñirse a este modelo, tal y como se plantea, es que el área de vista de la Tierra es infinita (y por ende los factores de vista prácticamente nulos) y que al intentar calcular los factores de vista, de todos modos la probabilidad de que un rayo impacte al satélite sería muy baja. Por ello se invierten nuevamente emisor y receptor: se disparan rayos desde los elementos del satélite y se consideran aquellos que no colisionan con otro elemento y cuyo ángulo con la dirección satélite-Tierra es menor a 90 grados o alternativamente, cuyo producto interno es mayor a cero.

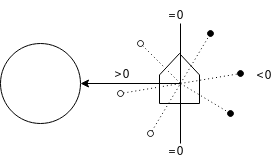
El cociente entre rayos que alcanzaron la Tierra y rayos totales es fue una buena primera aproximación del factor de vista elemento-Tierra para radiación, pero no considera la curvatura de la Tierra, ni el ángulo de incidencia del rayo en el elemento. Para incorporar ambos factores se acabó realizando el promedio ponderado de los rayos, tomando como peso la multiplicación del producto interno entre vector satélite-Tierra y rayo (que brinda información del punto de procedencia del rayo) y el producto interno entre la normal del elemento y el rayo (análogo a la corrección por área aparente solar):

\[ F^{\text{IR}}_{j} = \frac{1}{R _T} \sum^{R _I} _{i = 0} (r _i . v _{se})(r _i .n _j) \]

Donde:

\(F^{\text{IR}}_{j}\) es el factor de vista del elemento \(j\) a la Tierra para la radiación infrarroja.
\(R _T\) es la cantidad de rayos disparados por el método.
\(R _I\) es la cantidad de rayos disparados que impactaron a la Tierra.
\(r _i\) Es el iésimo rayo impactado.
\(v _{se}\) Es el vector unitario en dirección a la Tierra, tomando la posición del satélite como origen de coordenadas.
\(n _j\) Es la normal del elemento \(j\).

En órbitas sun pointing el satélite rota respecto a la Tierra, por lo que estos factores de vista sí deberán ser calculados para distintos puntos de la órbita.

Con el procedimiento descrito pudo estimarse la energía intercambiada por radiación infrarroja, pero para el albedo debió aplicarse una corrección adicional por cada rayo que impactó al satélite, dependiendo de si había sido emitido desde un punto de la Tierra que el Sol iluminaba o no.

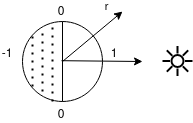
En principio, la Tierra puede considerarse como una esfera partida en dos, una semiesfera iluminada y otra en umbra. Los puntos de la semiesfera iluminada tienen un producto interno por el vector de la dirección solar positivo y los de la semiesfera en umbra un producto interno negativo.

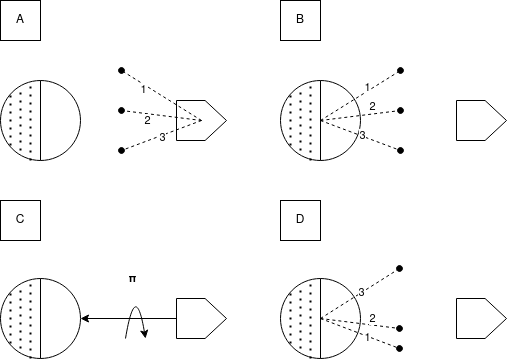
Como los rayos son emitidos desde el satélite hacia la Tierra en el cómputo, el producto interno debe invertirse. Además, es preciso rotar en 180 grados sobre el vector Tierra a satélite, ya que como puede observarse en el segundo caso, los rayos que provienen de zonas iluminadas o en umbra se intercambian si solo se invierte el sentido de los rayos.

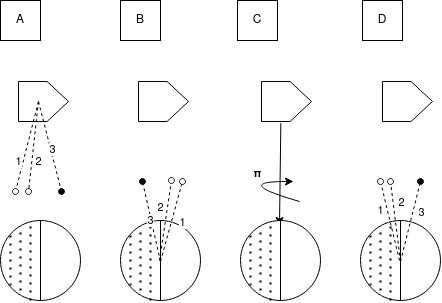
Es importante notar que la abrupta transición entre zonas iluminadas y en umbra es consecuencia del mapeo elegido entre producto interno e intensidad de luz (aquí la función de Heavyside). Puede suavizarse la transición entre zona iluminada y umbra e introducir así el efecto de scattering atmosférico, pero no se observó que impactase en los resultados significativamente.

\[ F^{Albedo}_{j} = \frac{1}{R _T} \sum^{R _I} _{i = 0} u(r _i.v _{es}) (r _i.v _{es}) (r _i .n _j) \]

Donde:

\(F^{Albedo}_{j}\) es el factor de vista del elemento \(j\) a la Tierra para la radiación por albedo.
\(R _T\) es la cantidad de rayos disparados por el método.
\(R _I\) es la cantidad de rayos disparados que impactaron a la Tierra.
\(r _i\) Es el iésimo rayo impactado, con la rotación mencionada ya aplicada.
\(v _{es}\) Es el vector unitario en dirección al Sol, tomando la posición de la Tierra como origen de coordenadas.
\(n _j\) Es la normal del elemento \(j\).
\(u \) Es la función de Heaviside.

Solver

El solver fue construido con el objetivo de realizar la simulación de la transferencia de calor del satélite en órbita, frente a la interacción con las fuentes de energía del Sol y la Tierra.

Dado que el rendimiento es un objetivo relevante de este software, se decidió hacer uso de Rust como lenguaje de programación para código a ser ejecutado en CPU, ya que brinda las facilidades de un lenguaje de programación moderno y, adicionalmente, ha demostrado tener tiempos de ejecución comparables a los de C en pruebas realizadas. Por otro lado, se eligió a OpenCL como lenguaje de programación del código a ser ejecutado en GPU debido a que permite lograr una abstracción completa del hardware subyacente. Esta plataforma es soportada no solo por distintos proveedores de tarjetas gráficas, sino también por distintos tipos de hardware, entre los que se pueden encontrar CPUs y tensores.

Como método numérico para el desarrollo del modelo se eligió FEM (Finite Element Method), debido a su conocida estabilidad numérica frente a geometrías diversas, su abundante bibliografía y por ser el método que usualmente se emplea para el cálculo de este tipo de problemas.

Modelo teórico

Transferencia de Calor

En lineas generales, la transferencia de calor puede explicarse a través de 3 fenómenos distintos: la conducción, la convección y la radiación.

Dado que la densidad del aire a altitudes muy elevadas es extremadamente baja, a partir de órbitas terrestres bajas (LEO) en adelante la transferencia de calor es, practicamente en su totalidad, debida a la conducción y radiación. Es por esto que, es posible omitir el fenómeno de convección en el modelo.

Sin convección natural para enfriar la electrónica, un sistema que funciona con la misma potencia en el espacio es más probable que alcance una temperatura más alta en comparación con uno que opera a nivel del mar.

Transferencia de Calor por Conducción

La transferencia de calor puede ocurrir dentro de un material o entre dos o más cuerpos en contacto. Está dada por la Ley de Fourier, en una dimensión:

\[ f^{''}_x = -k \frac{dT}{dx} \]

Donde:

\(q\) es la tasa de flujo de calor (\(\frac{W}{m^2}\))
\(k\) es la conductividad térmica (\(\frac{W}{m *K}\)) del material
\(\frac{dT}{dx}\) es la diferencia de temperatura a lo largo de la longitud

En el caso más general, la ecuación se expresa en forma diferencial

\[ c p \frac {\partial T}{\partial t} = k \ (\frac {\partial^2 T}{\partial x^2} + \frac {\partial^2 T }{\partial y^2} + \frac {\partial^2 T }{\partial z^2}) + q_v \]

Donde:

\(c\) es el calor específico \([\frac{J}{Kg \ K}]\)
\(p\) la densidad \([\frac{Kg}{m^3}]\)
\(q_v\) el calor generado \([\frac{W}{m^3}]\)

Transferencia de Calor por Radiación

La transferencia de calor por radiación ocurre entre dos o más superficies a través de ondas electromagnéticas. Depende de la temperatura y del revestimiento de la superficie radiante. El tipo de emisor más eficiente es conocido como cuerpo negro. La radiación que emite por unidad de área a una temperatura dada sigue la Ley de Stefan-Boltzmann.

\[ E = \sigma \ T^4 \]

Donde:

\(σ\) es la constante de Stefan-Boltzmann (\(5.63 \times 10^{-8} \frac{W}{m^2 K^4}\))
\(T\) es la temperatura del cuerpo negro \([K]\)

Multiplicando por el area radiante \(A^r\), se obtendrá el calor absoluto emitido por el cuerpo negro \(E_r [W]\):

\[ E_r = A^r \sigma \ T^4 \]

A un cuerpo que no irradia con la misma eficiencia que un cuerpo negro se lo conoce como cuerpo gris. La radiación emitida por un cuerpo gris hace uso de la ecuación de cuerpo negro, corregida por un factor de emisividad.

\[ E_{gris} = ε A^r \sigma \ T^4 \]

Donde:

\(ε\) es la emisividad del cuerpo gris

El calor transferido desde un cuerpo gris (1), hacia otro cuerpo gris (2) por radiación puede expresarse de la siguiente forma:

\[f_{1,2} = \sigma \ ε_1 \ \alpha_2 \ F_{1,2} \ A_1 \ T_1^4\]

Donde:

\(ε_1\) es la emisividad de la superficie del cuerpo 1.
\(\alpha_2\) es la absortividad de la superficie del cuerpo 2.
\(F_{1,2}\) es el factor de vista entre la superficie del cuerpo 1 y el cuerpo 2
\(A_1\) es el área de la superficie del cuerpo 1.
\(T_1\) es la temperatura del cuerpo 1.

El factor de vista de una superficie 1 hacia una superficie 2 se define como la porción del campo de visión de la superficie 1 que es ocupada por la superficie 2. Dado que se trata de un porcentaje, este toma valores entre cero y uno.

Así como el factor de emisividad corrige la diferencia de emisión de un cuerpo gris frente a la emisión teórica de un cuerpo negro, el factor de absortividad realiza la misma corrección sobre la cantidad de energía absorbida por la superficie de un cuerpo gris. Dado que ambos factores suelen ser similares (para una misma superficie), se suelen simplificar las ecuaciones reemplazando la emisividad por la absortividad. Es importante aclarar que tanto la absortividad como la emisividad dependen no solo de la superficie en cuestión, sino también de la frecuencia de la radiación emitida o recibida.

Fuentes de Calor en Sistemas Espaciales

En un sistema espacial existen, generalmente, tres fuentes de calor:

Radiación del sol.
Radiación de albedo.
Radiación infrarroja terrestre.

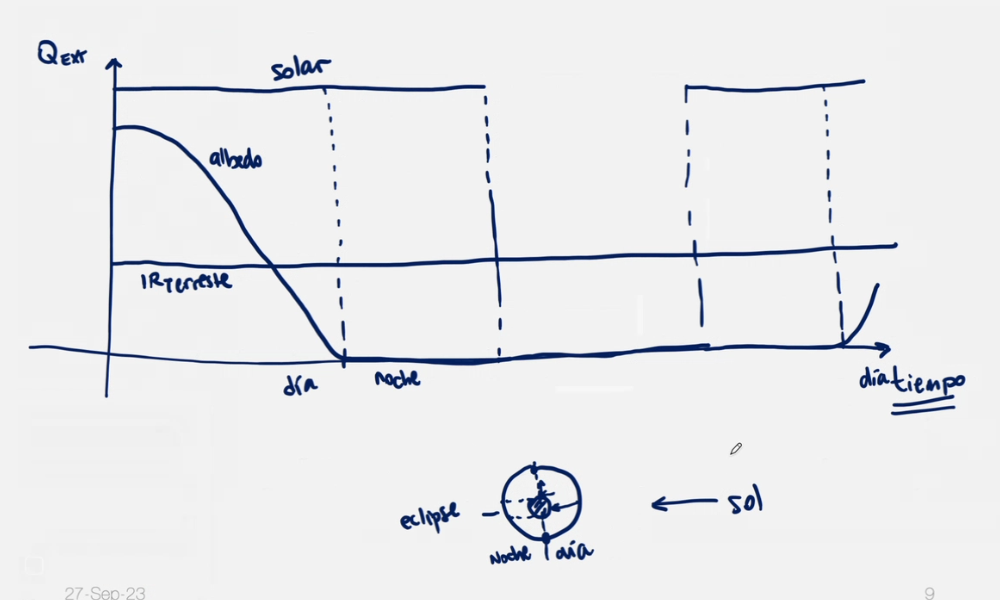
Radiación solar

Es la principal fuente de calor y puede ser considerada constante. Suele rondar entre 1322 \(\frac{W}{m^2}\) y 1414 \(\frac{W}{m^2}\).

La radiación proveniente desde el sol e incidente sobre una superficie se encuentra en función del flujo solar \(S \ [\frac{W}{m^2}]\) y de la orientación de esta con respecto al sol. Debido a la gran distancia con el sol, se puede tomar la suposición de que la radiación esta dada por rayos paralelos.

El calor recibido por una superficie \(i\) debido a la radiación proveniente del sol estará dado por:

\[ f_{Solar} = \alpha_i^{Sun} F_{Sun,i} \ A_i S \]

\(\alpha_i^{Sun}\) considera la absortividad de la superficie \(i\) bajo la frecuencia de las ondas electromagnéticas emitidas por el sol.

Albedo

El albedo refiere a la radiación solar reflejada desde la superficie terrestre. Se suele expresar como la fracción de radiación solar incidente que es reflejada hacia el espacio.

\[ f = A_f S\]

Donde:

\(A_f\) es el factor de albedo
S es la constante solar \([\frac{W}{m^2}]\)

El albedo promedio de la tierra es de aproximadamente 0.3.

De esta forma, es posible expresar el calor recibido por una superficie \(i\) debido al albedo de la siguiente forma:

\[ f_{Albedo} = \alpha_i^{Sun} F_{Earth,i} \ A_i A_{f_i} S \]

Radiación Infraroja Terrestre

La radiación Infraroja (IR) terrestre refiere a la radiación emitida por la tierra por el simple hecho de tratarse de un cuerpo con temperatura mayor a cero grados absolutos. Por lo general se considera que esta radiación es constante a lo largo de su superficie y se la suele tomar con un valor cercano a 235 \(\frac{W}{m^2}\).

El calor recibido por una superficie S debido a radiación IR estará dado por:

\[ f_{IR} = \alpha_i^{IR} F_{Earth,i} \ E_{IR} \]

Donde:

\(E_{IR}\) es la constante de IR terrestre \([\frac{W}{m^2}]\)

Transferencia de calor en el satelite

Además de recibir energía por radiación del sol y la tierra, un satélite emite hacia su alrededor.

Tratandose de un cuerpo gris, el flujo de calor emitido por una superficie del satélite estará dado por:

\[ f_{Lost} = \alpha^{IR} A^r \sigma \ T^4 \]

Parte de esta energía será perdida en el espacio y otra parte será absorbida por otras superficies del propio satélite. El flujo recibido por una superficie \(j\) del satélite, debido a la emisión de una superficie \(i\) estará dado por:

\[ f_{i,j}^{elem} = \sigma \ \alpha_i^{IR} \alpha_j^{IR} F_{i,j} A_i \ T_i^4 \]

Modelo FEM

Ecuación de Calor

Para resolver el problema de transferencia de calor se utilizó el método numérico de elementos finitos (FEM). Este método consiste en discretizar las superficies del dominio del problema a simular en elementos, cada uno de los cuales está compuesto por vértices o nodos de cómputo. El número de nodos por elemento dependerá de la forma de éste, pudiendo utilizar elementos rectangulares o triangulares. El desarrollo fue realizado utilizando estos últimos.

A continuación se presentará un resumen del método empleado. Para mas información sobre el desarrollo matématico referirse al paper Finite Element Method in Steady-State and Transient Heat Conduction.

Se comienza planteando la ecuación que gobierna la transferencia de calor en dos dimensiones:

\[ c p \frac {\partial T}{\partial t} = \frac {\partial }{\partial x} (k_x\frac {\partial T}{\partial x}) + \frac {\partial }{\partial y} (k_y\frac {\partial T}{\partial y}) + q_v \]

Donde:

\(c\) es el calor específico del material.
\(p\) la densidad del material.
\(k_x\) y \(k_y\) las conductividades térmicas del material en cada componente.

Esta ecuación se encuentra sujeta a tres tipos de condiciones de contorno:

Dirichlet: Temperatura conocida en una región.
Neumann: Flujo de calor conocido en una región.
Combinación Dirichlet y Neumann: Calor recibido debido a flujo de convección y temperatura ambiente conocidos en una región.

Debido a que el fenómeno de transmisión de calor por convección no se encuentra presente en el dominio del problema, la tercer condición es descartada. Adicionalmente, con el objetivo de simplificar el desarrollo del modelo, las primeras dos condiciones también son descartadas. Más adelante se detallará como se logró obtener el mismo efecto de la condición de Neumann por otro medio.

Y, por último, la condición inicial necesaria para resolver es:

\[T(x,y,t)|_{t=0} = T_0(x,y)\]

Representación Matricial

Tras desarrollar la ecuación presentada, aplicando las condiciones y discretización en elementos, se obtiene la siguiente ecuación:

\[ [M^e] {\frac {d T^e}{dt}} + [K^e] { T^e } = { f^e}\]

Donde:

\( [M^e] \) es la matriz de capacitancias.
\([K^e]\) es la matriz de conductividad.
\({ f^e}\) es el vector de flujos.

Esta ecuación matricial es conocida como la representación de Galerkin de la ecuación de transmisión de calor transitoria. Si las propiedades físicas \(k, \rho, c\) son independientes de la temperatura, entonces la misma puede ser resuelta utilizando métodos de resolución de sistemas de ecuaciones lineales. Las matrices que participan en esta ecuación hacen referencia a un único elemento de todo el dominio. A estas se las conoce como matrices locales.

Construcción de matrices locales

Las matrices locales antes presentadas son construidas de la siguiente forma:

Dado un elemento genérico

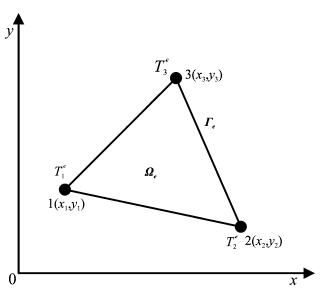
Tomando como hipótesis que la conductividad térmica del material es isotrópica (\(k_x = k_y = k\)). Es decir, los materiales poseen la misma conductividad en ambas direcciones. Y considerando que \(A^e\) es el area del elemento.

La matriz de conductividad del elemento \([K_c^e]\), tiene la forma

\[ [K_c^e] = \begin{bmatrix} K^e_{11} & K^e_{12} & K^e_{13}\\ K^e_{21} & K^e_{22} & K^e_{23}\\ K^e_{31} & K^e_{32} & K^e_{33} \end{bmatrix} \]

Donde:

\[ \begin{aligned} \begin{split} b_1 = y_2 - y_3 \\ b_2 = y_3 - y_1 \\ b_3 = y_1 - y_2 \end{split} \quad\quad \begin{split} c_1 = x_3 - x_2\\ c_2 = x_1 - x_3\\ c_3 = x_2 - x_1 \end{split} \end{aligned} \]

\[ \begin{aligned} \begin{split} K^e_{11} &= \frac{k}{4A^e} ({b_1}^2 + {c_1}^2) \\ K^e_{12} &= \frac{k}{4A^e} (b_1 b_2 + c_1 c_2) \\ K^e_{13} &= \frac{k}{4A^e} (b_1 b_3 + c_1 c_3) \end{split} \quad \begin{split} K^e_{21} &= K^e_{12} \\ K^e_{22} &= \frac{k}{4A^e} (b_2^2 + c_2^2) \\ K^e_{23} &= \frac{k}{4A^e} (b_2 b_3 + c_2 c_3) \end{split} \quad \begin{split} K^e_{31} &= K^e_{13} \\ K^e_{32} &= K^e_{23} \\ K^e_{33} &= \frac{k}{4A^e} (b_3^2 + c_3^2) \end{split} \end{aligned} \]

La matriz de capacitancia del elemento \([M^e]\), tiene la forma

\[ [M^e] = \frac{A^e}{12} c p \begin{bmatrix} 2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2 \end{bmatrix} \]

El vector de flujo debido a generación de calor interna \({f^e}\), tiene la forma

\[ {f^e} = q \frac{A^e}{3} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \]

Donde \(q\) es el calor generado dentro del elemento.

Construcción de matrices globales

Hasta el momento se han detallado las ecuaciones y matrices empleadas a nivel local, dentro de un único elemento. A continuación se detallará cómo es posible expandir este modelo al resto de los elementos.

Se parte de un ejemplo de un modelo con 2 elementos y 4 nodos. A cada nodo se le asignará una numeración local, que lo identifica dentro de un mismo elemento, y una numeración global, que lo identifica frente al resto de nodos del modelo.

La numeración global es la siguiente:

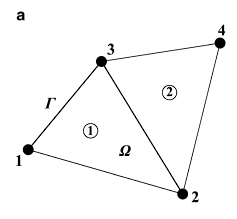
Y la numeración local:

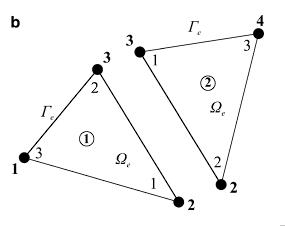
El proceso de construcción de una matriz global consiste en utilizar los identificadores globales de los nodos de cada matriz local para agregar los resultados en la matriz global. De esta forma, por cada coordenada \((x,y)\) de identificadores locales dentro de una matriz local existirá un mapeo a una coordenada \((u,v)\) de identificadores globales en la matriz global.

Por tomar un ejemplo, en el elemento número 1, el nodo de identificador local 1 tiene asignado un identificador global 2. Por ende, su mapeo será \((1, 1) \rightarrow (2, 2)\).

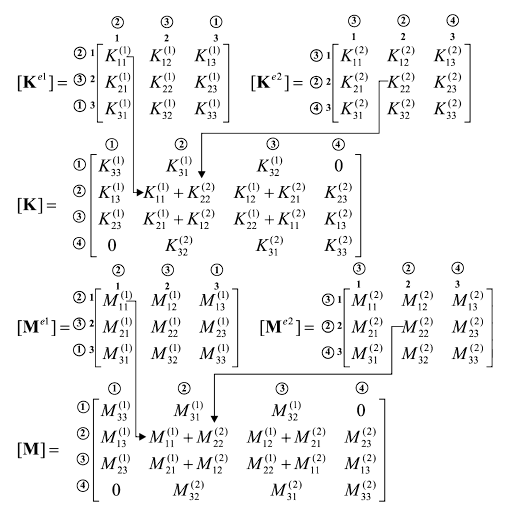
De forma análoga es posible construir el vector de flujos global

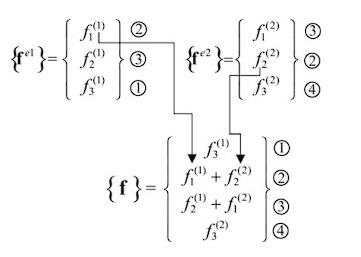
Una vez obtenidas las matrices globales, es posible expandir la ecuación de Galerkin a su forma global.

\[[M] {\frac {d T}{dt}} + [K] { T } = { f}\]

Luego, si esta ecuación es discretizada en función del tiempo haciendo uso del método de Crank-Nicolson generalizado, se obtiene

\[ (\frac{1}{\Delta t}[M] + \theta [K] ) \ { T }^{n+1} = (\frac{1}{\Delta t}[M] - (1 - \theta) [K]) \ {T}^n + (1 - \theta) {f}^n + \theta {f}^{n+1} \]

Eligiendo \(\theta = 0.5\) se obtiene el conocido esquema semi-implícito por método de Crank-Nicolson.

Adicionalmente, en pos de mantener la linealidad de la ecuación al añadir a esta los términos cuarticos referentes a radiación, se decidió hacer uso de una corrección del método tal que se eliminase su característica implícita en el vector de flujos.

En esta modificación se asume para el instante \(n\), que el flujo permanecerá constante en el instante siguiente. Esto es:

\[ {f}^n = {f}^{n+1} \]

Por lo que la ecuación puede reescribirse de la siguiente forma:

\[ (\frac{1}{\Delta t}[M] + \theta [K]) \ { T }^{n+1} = (\frac{1}{\Delta t}[M] - (1 - \theta) [K]) \ {T}^n + {f}^n \]

Expansión a tres dimensiones

Todo el desarrollo hasta el momento ha sido planteado desde el punto de vista de un modelo 2D. A continuación se explicará como es posible seguir utilizando el mismo modelo, con pequeñas correcciones, para simular la propagación de calor sobre la superficie de objetos 3D. A este tipo de modelo, que no contempla transmisión a nivel volumétrico, se lo suele llamar 2.5D.

Los cambios a realizar implican incorporar un parámetro de grosor \(G_e\) para cada elemento (asociado a una superficie) e incrementar la dimensionalidad de los puntos del modelo de 2 a 3 coordenadas \((x, y, z)\).

Tras aplicar estos cambios será necesario modificar la forma en la que algunas matrices locales son construidas.

La matriz de capacitancia será multiplicada por el grosor del elemento.

\[[M^e] = \frac{A^e}{12} G_e c \rho \begin{bmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{bmatrix} \]

Por otro lado, la matriz conductividad también será multiplicada por el grosor del elemento, pero además verá modificada las constantes que dan lugar a su creación.

Observese que los calculos de las constantes \(b_i\) y \(c_i\) refieren a propiedades espaciales del elemento. La operación \(b_1^2 + c_1^2\) no es más que la distancia al cuadrado entre el vertice 2 y el vertice 3 del elemento. Por otro lado, la operación \(b_1 b_2 + c_1 c_2\) se puede interpretar como el producto escalar entre dos vectores, el primero es el que une el vertice 2 con el vertice 3, y el segundo el que une el vertice 3 con el vertice 1.

Por lo tanto, todos estos calculos pueden realizarse a partir de las coordenadas de los vertices en 3D. De esta forma, la matriz de conductividad puede ser construida de la siguiente forma:

\[ [K_c^e] = \begin{bmatrix} K^e_{11} & K^e_{12} & K^e_{13}\\ K^e_{21} & K^e_{22} & K^e_{23}\\ K^e_{31} & K^e_{32} & K^e_{33} \end{bmatrix} \]

Donde:

\[ \begin{aligned} \begin{split} K^e_{11} &= G_e \frac{k}{4A^e} ||v_3 - v_2||^2 \\ K^e_{12} &= G_e \frac{k}{4A^e} (v_3 - v_2) \cdot (v_1 - v_3) \\ K^e_{13} &= G_e \frac{k}{4A^e} (v_3 - v_2) \cdot (v_2 - v_1) \end{split} \quad \begin{split} K^e_{21} &= K^e_{12} \\ K^e_{22} &= G_e \frac{k}{4A^e} ||v_3 - v_1||^2 \\ K^e_{23} &= G_e \frac{k}{4A^e} (v_1 - v_3) \cdot (v_2 - v_1) \end{split} \quad \begin{split} K^e_{31} &= K^e_{13} \\ K^e_{32} &= K^e_{23} \\ K^e_{33} &= G_e \frac{k}{4A^e} ||v_2 - v_1||^2 \end{split} \end{aligned} \]

Siendo \(v_1, v_2, v_3\) los vértices del elemento.

Incorporación de radiación

Ya habiendo conseguido un modelo que permite simular la transferencia de calor debido a conducción, queda añadir a este la capacidad de transmitir energía debido a radiación.

Las ecuaciones que modelan la radiación para un sistema espacial son, según lo detallado en la sección anterior:

\begin{equation} \begin{aligned} & Q_{Solar} = \alpha_i^{Sun} F_{Sun,i} \ A_i S \\[10pt] & Q_{Albedo} = \alpha_i^{Sun} F_{Earth,i} \ A_i A_{f_i} S \\[10pt] & Q_{IR} = \alpha_i^{IR} F_{Earth,i} \ E_{IR} \\[10pt] & Q_{Lost} = \alpha^{IR} A^r \sigma \ T^4 \\[10pt] & Q_{i,j}^{elem} = \sigma \ \alpha_i^{IR} \alpha_j^{IR} F_{i,j} A_i \ T_i^4 \\[10pt] \end{aligned} \end{equation}

A continuación se buscará reescribir estas ecuaciones en función de los elementos y nodos del método FEM, haciendo uso de representaciones matriciales locales y/o globales.

De forma sencilla se pueden obtener las siguientes representaciones locales para un elemento \(e\):

\[ \begin{aligned} & {f^e_{Solar}} = \alpha_e^{Sun} F_{Earth,e} \frac{A_e}{3} S \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \\[10pt] & {f^e_{Albedo}} = \alpha_e^{Sun} F_{Sun,e} A_{f_e} \frac{A_e}{3} S \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \\[10pt] & {f^e_{IR}} = \alpha_e^{IR} F_{Earth,e} \frac{A_e}{3} E_{IR} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \\[10pt] & {f^e_{Lost}} = \sigma \ \alpha_e^{IR} \frac{A_e}{3} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} {T_1^e}^4 \\ {T_2^e}^4 \\ {T_3^e}^4 \end{bmatrix} \end{aligned} \]

Cada una de estas matrices se puede expandir a una matriz global aplicando el método explicado anteriormente.

De todas las ecuaciones presentadas, la única que no posee representación matricial local es la ecuación de transmisión de calor entre elementos. Dicha ecuación posee únicamente una representación global que se detalla a continuación.

\[ L = \frac{\sigma}{3} \begin{bmatrix} L_{11} & L_{12} & \dots & L_{1n} \\ L_{21} & L_{22} & \dots & L_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ L_{n1} & L_{n2} & \dots & L_{nn} \end{bmatrix} \qquad \]

Donde:

\[ L_{i,j} = \sum_{k = Elem(i)} \sum_{w = Elem(j)} P_{w,k} \\[20pt] i,j \in \{1 \ .. \ N\} \\[10pt] N: \textit{Número de nodos} \\[10pt] L_{i,j}: \textit{Energía emitida por el nodo j, recibida por el nodo i}\\[10pt] Elem(i): \textit{Conjunto de los elementos a los que pertenece el nodo i}\\[20pt] \]

\[ P_{w,k} = F_{w,k} \ \alpha_w^{IR} \ \alpha_k^{IR} \ A_w \\[10pt] w,k \in \{1 \ .. \ V\} \\[10pt] V: \textit{Número de elementos} \\[10pt] P_{w,k}: \textit{Energía emitida por el elemento w, recibida por el elemento k} \]

De esta forma, queda definido el flujo de calor entrante por transmisión entre elementos:

\[ {f_{Elem}} = \frac{\sigma}{3} L \begin{bmatrix} {T_1}^4 \\ {T_2}^4 \\ \vdots \\ {T_n}^4 \end{bmatrix} \]

Uniendo las partes

Es posible reescribir la ecuación de Galerkin semi-implícita de la siguiente forma:

\[ [A] \ { T }^{n+1} = [D] \ {T}^n + {C}^n \]

Tal que:

\[ [A] = \frac{1}{\Delta t}[M] + \theta [K] \\[10pt] [D] = \frac{1}{\Delta t}[M] - (1 - \theta) [K] \\[10pt] C^n = f_{Gen} + f_{Solar} + f_{IR} + f_{Albedo} + f_{Elem} - f_{Lost} \\ \]

Donde \(f_{Gen}\) es el vector constante de generación interna de calor a nivel elemento, cuya representación local es:

\[ {f^e_{Gen}} = q \frac{A^e}{3} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \]

El vector \(C^n\) puede reescribirse de la siguiente forma:

\[ C^n = f_{Const} + [H]
\begin{bmatrix} {T_1}^4 \\ {T_2}^4 \\ \vdots \\ {T_n}^4 \end{bmatrix} \]

Donde:

\[ f_{Const} = f_{Gen} + f_{Solar} + f_{IR} + f_{Albedo} \\[10pt] [H] = [L] - [E] \\[10pt] [E] = \sigma \ \alpha_e^{IR} \frac{A_e}{3} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

Tal que:

\[ {f^e_{Lost}} = E \begin{bmatrix} {T_1^e}^4 \\ {T_2^e}^4 \\ {T_3^e}^4 \end{bmatrix} \]

De esta forma, al resolver el siguiente sistema de ecuaciones lineales para \(T^{n+1}\) se obtendrán los valores de las temperaturas de los nodos del modelo para un paso de tiempo.

\[ [A] \ { T }^{n+1} = [D] \ {T}^n + {C}^n \]
Repetir este procedimiento de forma iterativa dará como resultado una simulación de la transferencia y propagación del calor en el satélite en función del tiempo, dadas las condiciones configuradas.

Resolución de sistemas de ecuaciones

Existen distintas técnicas para resolver sistemas de ecuaciones lineales. La más sencilla de todas implica hacer uso de la inversa de la matriz de coeficientes.

Dado el sistema de ecuaciones lineales

\[ [A] \ {x} = {b} \]

Se obtiene el vector incógnita multiplicando el vector de términos constantes por la inversa de la matriz de coeficientes

\[ {x} = [A^{-1}] \ {b} \]

Esta técnica tiene un punto positivo y uno negativo. Como punto positivo, una vez obtenida la inversa, esta puede ser utilizada tantas veces como sea necesario para iterar sobre la simulación y obtener las temperaturas de los nodos en cada paso de tiempo con una simple multiplicación. Como punto negativo, el algoritmo para computar la inversa requiere realizar un aproximado de \(2n^3\) operaciones para una matriz de \(n \times n\).

Una alternativa a este método es hacer uso de una descomposición LU, en la cual la matriz de coeficientes es descompuesta en dos matrices auxiliares L y U.

Dado el sistema de ecuaciones lineales \[ [A] \ {x} = {b} \]

Se realiza una descomposición de la matriz de coeficientes en una matriz L triangular inferior, y una matriz U triangular superior.

\[ [A] = [L] \ [U] \]

Reemplazando en el sistema de ecuaciones

\[ [L] \ [U] {x}= {b} \]

Que puede ser reescrito de la siguiente forma

\[ \begin{aligned} &[L] \ {y} = {b}\\[6pt] &[U] \ {x} = {y}\\ \end{aligned} \]

Por ende, resolviendo secuencialmente ambos sistemas de ecuaciones, se podrá obtener la solución al sistema original. Ahora bien, gracias a que las matrices L y U son triangular inferior y superior respectivamente, es posible resolver ambos sistemas de ecuaciones en aproximadamente \(2n^2\) operaciones.

Por otro lado, el coste computacional de realizar la descomposición LU es de aproximadamente \(\frac{2}{3}n^3\) operaciones.

De esta forma, el costo computacional total para resolver el sistema de ecuaciones para una matriz de \(n \times n\) será:

\[ \sim \frac{2}{3}n^3 + 2n^2 \]

Esta técnica, al igual que la anterior, tiene un punto positivo y otro negativo. Como punto positivo, obtener la factorización LU es unas 3 veces más rápido que obtener la inversa de la matriz de coeficientes. Como punto negativo, cada vez que se requiera despejar un nuevo vector incógnita será necesario resolver los dos sistemas de ecuaciones de las matrices L y U antes detallado.

Otros algoritmos de resolución por métodos iterativos, como son el método de Jacobi, Gauss-Seidel y SOR también han sido estudiados. Sin embargo, todos ellos fueron descartados rápidamente, ya que requieren que la matriz de coeficientes sea diagonalmente dominante, característica que no puede ser asegurada para el dominio de este trabajo.

Resolución en CPU

La ejecución del solver puede dividirse en dos etapas. Por un lado, se tiene la construcción de los datos necesarios para iniciar la simulación, esto es, las matrices y vectores locales y globales antes mencionados. Por el otro lado se tiene la propia ejecución de la simulación, resolviendo la ecuación principal en cada iteración de la misma.

Con el objetivo de contrastar los métodos de inversión de matriz y descomposición LU para la resolución del sistema de ecuaciones, se realizó una prueba sencilla, haciendo uso de un cubo de aproximadamente 10000 elementos y 5000 nodos. Sobre este modelo se realizó una simulación que consistió en 6000 pasos o iteraciones, totalizando 30000 segundos de simulación.

Como resultado se obtuvo que, para la etapa de construcción el algoritmo de LU fue un 6% más lento que el algoritmo de inversión, mientras que para la etapa de simulación el algoritmo de inversión demoró un 131% más. Esto se traduce en un speedup de 49% a favor del algoritmo de descomposición LU. Adicionalmente, se compararon los resultados obtenidos entre ambos métodos y se computó el error absoluto medio, obteniendo un error de 0.04%. Esto demuestra que, al menos para el dominio del problema, ambos métodos poseen la misma estabilidad numérica.

En base a esto fue que se decidió hacer uso del método de descomposición para la implementación del solver sobre CPU.

Resolución en GPU

Llegado este punto se tiene una implementación funcional del solver que permite realizar simulaciones haciendo uso de la CPU. A partir de ahora, se buscará desarrollar una implementación que aproveche la potencia de la GPU, con la finalidad de reducir significativamente los tiempos de ejecución.

En contraste con las CPUs, las GPUs cuentan con un gran número de núcleos de ejecución. Una GPU moderna puede superar fácilmente los 3.000 núcleos, en comparación con los 12 núcleos de una CPU del mismo año. Sin embargo, es importante tener en cuenta que los núcleos de las GPUs son individualmente más simples y lentos en comparación con los núcleos de las CPUs. Además, se debe considerar la latencia en la transferencia de datos entre la memoria principal (RAM) y la memoria del dispositivo (GPU). Estas consideraciones se pueden resumir en las siguientes heurísticas clave al buscar optimizar la programación para GPU:

El programa debe poder ser descompuesto en porciones capaces de ser ejecutadas de forma paralela.
Se debe evitar interrumpir la ejecución de la GPU con transferencias entre la memoria principal y la memoria del dispositivo.
Se deben limitar lo máximo posible los accesos del programa a memoria del dispositivo.

Los programas destinados a GPUs suelen ser mayoritariamente codificados en lenguajes basados en C, con pequeñas variaciones que añaden funcionalidades específicas, como la obtención de identificadores de proceso o la sincronización entre procesos. Estos programas se componen principalmente de funciones conocidas como kernels. Para la programación en GPU, se ha optado por el estándar multiplataforma y de código abierto OpenCL, haciendo uso de la biblioteca ocl de Rust como binding.

Como se ha mencionado, el solver puede dividirse en dos etapas: la construcción de los datos necesarios para la simulación y la ejecución propiamente dicha de la simulación. Esto implica que existen dos oportunidades distintas para lograr un aumento en la velocidad, especialmente si estas etapas son llevadas a cabo en una GPU.

El algoritmo de descomposición LU utilizado en la implementación para CPU presenta un comportamiento secuencial en la fase de solución de las ecuaciones lineales sobre las matrices triangulares. Esta característica reduce cualquier potencial mejora obtenida mediante la paralelización de operaciones en la GPU. Por este motivo, se tomó la decisión de implementar la solución en GPU utilizando el método de inversión de matriz.

El desarrollo de este método se dividió en dos fases. La primera tuvo como objetivo la inversión de la matriz de coeficientes, mientras que la segunda se dedicó a implementar las operaciones necesarias para realizar la simulación en la GPU.

En cuanto a la inversión de la matriz, se exploraron varios algoritmos, siendo el algoritmo de Gauss-Jordan el más destacado debido a su simplicidad y capacidad de paralelización. Sin embargo, debido a errores de concurrencia en la implementación este algoritmo aún no se encuentra integrado en el software.

Para la segunda etapa se implementaron kernels basados en las funciones de GeMM (General Matrix Multiply), provenientes de la conocida biblioteca de álgebra lineal BLAS.

Los kernels implementados fueron:

__kernel void fourth_elevation(
    __global double *t, 
    __global double *t_4, 
    int n
);

__kernel void gemv1(
    __global const double *a, 
    __global const double *x, 
    __global double *y, 
    int m, 
    int n
);

__kernel void vec_sum(
    __global double *a, 
    __global double *b, 
    __global double *c, 
    int n
)

El kernel fourth_elevation recibe un vector de tamaño \(n\) conteniendo las temperaturas de los nodos y escribe el resultado de elevar cada componente de éste en el vector t_4 del mismo tamaño. Para su ejecución se divide el trabajo en \(n\) work items.

El kernel gemv1 realiza la multiplicación de la matriz a de dimensionalidad \(m \times n\) por el vector x, escribiendo el resultado en el vector y. Aquí se hace uso de una versión simplificada del algoritmo GEMM antes mencionado. Para su ejecución se divide el trabajo en \(m\) work items, cada uno de las cuales realiza el cómputo de una fila de la matriz a.

El kernel vec_sum realiza una suma entre los dos vectores a y b de tamaño \(n\) y escribe el resultado en el vector c. Para su ejecución se divide el trabajo en \(n\) work items.

Al momento de ejecutar la simulación, las operaciones generadas son encoladas por parte de la CPU a una cola de trabajo que provee OpenCL como medio de comunicación con la GPU. Gracias a la forma en la cual las operaciones fueron construidas, es posible ejecutar varias iteraciones de la simulación sin necesidad de realizar transferencias de datos entre la memoria de la GPU y la memoria principal. Antes de comenzar la ejecución, el programa en CPU calcula el número de iteraciones a realizar y encola exactamente el número de operaciones acordes a este, tal que la GPU se mantenga ocupada de manera ininterrumpida. El número de iteraciones a realizar estará relacionado con la necesidad de obtención de resultados parciales por parte de la CPU, o a la actualización del vector de flujos constante, el cual tiene dependencias con la posición del satélite en la órbita.